# A tibble: 6 × 3
name height weight
<chr> <dbl> <dbl>
1 A01 147. 52.3
2 A02 150. 53.2
3 A03 152. 54.5
4 A04 155. 55.9
5 A05 158. 57.3
6 A06 160 58.68 回帰分析(1)
回帰分析とは、データの中のある値を他の変数の重みつきの線形結合によって 表現しようとする方法である。この章では説明変数が1つの 単回帰分析を中心に説明する。係数がどのようなときに求まるのか、また 当てはまりの評価の方法について述べる。
キーワード
単回帰分析、決定係数、説明変数、目的変数、 サンプルサイズ
8.1 単回帰分析
回帰分析とは、求めたい値をその他の値を用いて表そうとする方法のことである。 例えば、ある人の身長を聞けば、その人が標準的な体型ならば、その人の体重をある程度の精度で予測することができるだろう。 これは、体重を身長の値を使って表す式を求めていることになる。これが回帰直線である。 このとき、身長だけといったように 1つの変数で表そうとするものを単回帰分析といい、 2つ以上の説明変数を用いる場合を重回帰分析(multiple regression analysis)という。 身長と体重のデータ(sreg.csv)を見てみよう。これは(Figure 8.1) のように表すことができる。点はほぼ一直線上に並んでいる。
図示すると次のようになる。

これをみると身長の値を教えてもらうだけで、その人の体重を求めることがで きると考えることができるだろう。 そのためには、身長 \(X\) cm、体重 \(Y\) kgに対して、 \(Y=aX+b\) となるような \(a\)、\(b\)を求めることを考えてみよう。 ここで、この身長の\(X\)の値を説明変数 (explanatory variable)といい、体重の\(Y\)のことを目的変数(response variable)という。 回帰分析とは目的となる変数を説明変数を用いて説明する、そのような直線(一般には超平面)の式を 求めることである。このような直線とは、すべてのデータの特徴を表す式であると考えることもできる。 さて、(Figure 8.2) のように \(N\) 個の観測したデータの組のサイズ (以降これをサンプルサイズという) \[ (x^{(1)},y^{(1)}),\cdots,(x^{(p)},y^{(p)}),\cdots,(x^{(N)}、y^{(N)})\] があるとしよう。 \(x^{(1)}\) をもとに計算した \(ax^{(1)}+b\) と \(y^{(1)}\) の値と近ければよい。 そこで、実際の値 \(y^{(1)}\) との違いである長さが最小となるように \(a\)、\(b\)を求めてみよう。
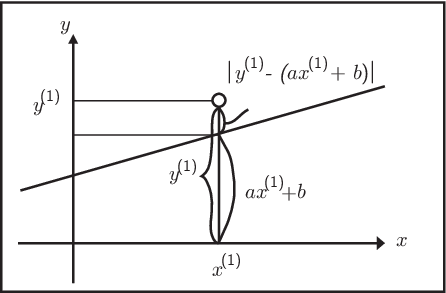
そこで実際の値と計算した値の差の2乗を誤差として、すべて足し合わせる。
\[\begin{eqnarray} \nonumber E &=&\left(y^{(1)}-(ax^{(1)}+b) \right)^2 +\cdots+\left(y^{(N)}-(ax^{(N)}+b)\right)^2 \\ &=& \sum_{p=1}^{N}\left( y^{(p)}-(ax^{(p)}+b)\right)^2 \end{eqnarray}\]これが最小になる \(a\)、\(b\)を求めてみよう。 このように 2乗の和を最小にすることによって、\(a\)、\(b\)を求める方法を 最小2乗法という。両辺をそれぞれ \(a\)、\(b\) で偏微分すると
\[\begin{eqnarray} \sum_{p=1}^{N}\left(y^{(p)}- ax^{(p)}-b\right)x^{(p)}&=&0 \\ \sum_{p=1}^{N}\left(y^{(p)}-a x^{(p)}-b\right)&=&0 \end{eqnarray}\]となる。上の式\(N\)で割ると、 \[\mu_y-(a\mu_x+b) =0\] である。\(\mu_x\)、\(\mu_y\)はそれぞれの平均であるとする。 回帰直線はそれぞれの平均を通る直線 \[y-\mu_y = a (x-\mu_x)\] であることがわかる。 そこで、すべての点を中心化して
\[\begin{eqnarray} {x^{(p)}}^{\prime} &=& x^{(p)}-\mu_x \\ {{y}^{(p)}}^{\prime}&=& y^{(p)}-\mu_y \end{eqnarray}\]とすると、
\[\begin{eqnarray} E &=& \sum_{p=1}^{N} \left({{y}^{(p)}}^{\prime}-a{x^{(p)}}^{\prime}\right)^2 \end{eqnarray}\]となるので、
\[\begin{eqnarray} 0&=& \sum_{p=1}^{N}\left({{y}^{(p)}}^{\prime}- a{x^{(p)}}^{\prime}\right) {x^{(p)}}^{\prime} \end{eqnarray}\]から \[ S_{xy}-a S_{xx}=0 \] が得られる。これより、\(S_{xx}\neq 0\)であれば、最終的に \(a\)、\(b\) を求めることができる。 ここで、\(S_{xx}\)や \(S_{xy}\) をサンプルサイズから1を引いた \(N-1\) で割ったものが分散共分散である。 とすると, \(S_{xx}= 0\) とは ばらつきがないということであり、 \(N\)個の \(x^{(p)}\) がどれも同じ値であることを意味している。 もし、それぞれの\(y^{(p)}\)の値が異なるとすると、 入力がどれも同じなのに、出力が異なる値であるときに、 \(y\) を予測することは考えにくい。 \(S_{xx} \neq 0\)として考えればよい。 この連立方程式を解くと、 \[ a=\frac{S_{xy}}{S_{xx}}\] \[ b=-\frac{S_{xy}}{S_{xx}}\mu_x+\mu_y \] と求めることができる。
8.2 重回帰分析
\(r\)個の説明変数の場合、\(y\)を求める式は \[
Y=a_1X_1+a_2X_2+\cdots+a_rX_r+b=\sum_{i=1}^{r}a_iX_i+b
\] と書くことができる。 この式は個々の変数\(x_i\)の1次式で表されている。 これを線形結合という。 また、この係数 \(a_{1}\)、\(a_{2}\)、\(\cdots\)、\(a_{r}\)を 偏回帰係数という。
ここでは、偏回帰係数を \(N\) 個のデータ \[
(x_1^{(1)},x_2^{(1)},\cdots、x_r^{(1)}),
(x_1^{(2)},x_2^{(2)},\cdots,x_r^{(2)}),
\cdots
(x_1^{(N)},x_2^{(N)},\cdots,x_r^{(N)})
\] から求める。 今、求めたい変数の数は、\(a_{i}\) 及び \(b_j\)の数で \(r+1\)個である。これを \(N\)個の数から求めるので、 \(N\) が \(r\) より小さいと係数を求めることができない。 \(N\) の数は \(r\) に比べて大きいものであるとする。 こうした条件のもとで単回帰のときと同様に計算しよう。 \(\mu_{x_i}\) を \(\mu_{i}\)、\(S_{x_ix_j}\) を \(S_{ij}\) とすると
という連立方程式が得られる。これを正規方程式 (normal equation) という。 ここで、 サンプルサイズ\(N-1\)で割ると\(X_i\)と\(X_j\)の共分散 \(\sigma_{x_ix_j}\)となる。これを \(\sigma_{ij}\)と略すと
\[\begin{eqnarray} \left( \begin{array}{cccc} \sigma_{11}&\sigma_{12}&\cdots& \sigma_{1r} \\ \sigma_{21}&\sigma_{22}&\cdots&\sigma_{2r} \\ \vdots&\vdots& \ddots& \vdots \\ \sigma_{r1}&\sigma_{r2}&\cdots& \sigma_{rr} \ \end{array} \right) \left( \begin{array}{c} a_{1} \\ \vdots \\ a_{r} \\ \end{array} \right ) &=& \left( \begin{array}{c} \sigma_{1Y} \\ \vdots \\ \sigma_{rY} \\ \end{array} \right ) \end{eqnarray}\]と書くことができる。 このように \(x_i\) と \(y\) の平均、分散、共分散を求めておくと、 の連立方程式を解くことで \(a_i\)を求まる。 さらに最後の式から \(b_j\) が求める。 ここで、もともとの重回帰式に代入すると、
\[\begin{equation} y-\mu_y = a_1(x_1-\mu_{1})+a_2(x_2-\mu_{2})+\cdots +a_r(x_r-\mu_{r}) \end{equation}\]となり、重回帰式は各変数の平均の点を通ることを意味している。 以上のことより、それぞれの変数の平均、分散共分散を求める。 分散共分散行列が逆行列を持てば、この重回帰式を求めることができることが分かる。
前節では \(r\)個の説明変数 \(a_i\) と切片 \(b\) を用いて説明したが、説明変数として \(x_0 = 1\) を加えた式として見る見方もある。 見やすくするために、\(m=r+1\) として、 \(i=0,1,\cdots,r\) に対し \(\phi_i=x_{i+1}\)、\(w_{i}=a_{i+1}\) とすると
\[\begin{equation} y^{(p)}=\sum_{i=1}^{m}w_i\phi_i^{(p)} \end{equation}\]と書き換えることができる。すると最小2乗法から導かれる式は
\[\begin{eqnarray} \boldsymbol{w}= \left( \begin{array}{c} w_1 \\ w_2 \\ \vdots \\ w_m \\ \end{array} \right) , \boldsymbol{\Phi} =\left( \begin{array}{cccc} \phi_1^{(1)}&\phi_2^{(1)}&\cdots&\phi_m^{(1)} \\ \phi_1^{(2)}&\phi_2^{(2)}&\cdots&\phi_m^{(2)} \\ \vdots & \vdots & \vdots & \vdots \\ \phi_1^{(N)}&\phi_2^{(N)}&\cdots&\phi_m^{(N)} \end{array} \right) , \boldsymbol{y}= \left( \begin{array}{c} y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(N)} \\ \end{array} \right) \end{eqnarray}\]とすると、正規方程式は
\[\begin{equation} (\boldsymbol{\Phi}^T \boldsymbol{\Phi}) \boldsymbol{w} =\boldsymbol{\Phi}^T \boldsymbol{y} \end{equation}\]と書くことができ、回帰係数は
\[\begin{equation} \boldsymbol{w} = (\boldsymbol{\Phi}^T \boldsymbol{\Phi})^{-1} \boldsymbol{\Phi}^T \boldsymbol{y} \end{equation}\]と書くことができる。
8.3 予測の正確さ
重回帰式の係数を求める方法について説明し、 分散共分散行列が逆行列を持てば係数を求めることができるということを述べた。 単に計算するのであれば、このように係数を定めることはできる。 しかし、値が求まったからそれでよいというわけではない。 はたしてどれだけ正確な予測をできるようになったのかを考えてみよう。 ある2つの確率変数があり、 \[ Y=0.2X+s\epsilon \] という関係があるとする。\(X\)、\(Y\) についてのデータ\((x^{(p)}、y^{(p)})\)を 入手して、データから\(X\)、\(Y\)の関係を求めることを考える。 \(\epsilon\) を標準正規分布に従う乱数であるとする。以降、\(s\epsilon\) の項をノイズと呼ぶ。この\(s\)はノイズのばらつきを表す値で これをノイズの大きさと呼ぶことにする。 このノイズの大きさを少しずつ変化させることを考える。 それによって、予測がどのように変わっていくのかについて見てみたい。 \(X\) は\(0\) から \(1\) の間で一様分布でランダムに取り出すことにする。 たとえば、\(s=0.1\) とすると次のように予測できる。
先ほどの回帰の式を解くことによって得られる \(a_i\) \(b\)のことを特に \(\hat{a_i}\)、 \(\hat{b}\)とし、これによって予測される値を \(\hat{y}^{(p)}\)とする。 最小2乗法といっても必ずしも誤差が \(0\) になるわけではない。そこで予測誤差を \(e^{(p)}\) とすると、
\[\begin{eqnarray} \hat{y}^{(p)} &=& \sum_{i=1}^{r}\hat{a_i}x_i^{(p)}+\hat{b} \\ &=& \sum_{i=1}^{r}\hat{a_i} \left(x_i^{(p)}-\mu_i\right)+\mu_y \\ {y}^{(p)}&=&\hat{y}^{(p)}+e^{(p)} \end{eqnarray}\]と書くことができる。そこで、予測誤差の2乗和を計算すると、
\[\begin{eqnarray} \sum_{p=1}^{N}(e^{(p)})^2 &=& \sum_{p=1}^{N} \left\{(y^{(p)}-\mu_y ) -\left( \sum_{i=1}^{r}\hat{a_i} \left(x_i^{(p)}-\mu_{i}\right) \right) \right\}^2 \\ &=& \sum_{p=1}^{N} (y^{(p)}-\mu_y)^2+ \sum_{p=1}^{N} \left( \sum_{i=1}^{r} \hat{a_i}(x_i^{(p)}-\mu_i) \right)^2 \\ && - 2 \sum_{p=1}^{N} \sum_{i=1}^{r} \hat{a_i} (x_i^{(p)}-\mu_{i})(y^{(p)}-\mu_y) \end{eqnarray}\]ここで、
\[\begin{eqnarray} \mbox{(上式第3項)} &=& \sum_{p=1}^{N} \sum_{i=1}^{r} \hat{a_i} \sum_{j=1}^{r} \hat{a_j}(x_i^{(p)}-\mu_i)(x_j^{(p)}-\mu_{j}) \\ &=& \sum_{p=1}^{N} \left( \sum_{i=1}^{r} \hat{a_i} (x_i^{(p)}-\mu_i) \right)^2 \end{eqnarray}\]である。最終的に \[ \sum_{p=1}^{N}(e^{(p)})^2 = \sum_{p=1}^{N} (y^{(p)}-\mu_y)^2 - \sum_{p=1}^{N} \left( \sum_{i=1}^{r} \hat{a_i}(x_i^{(p)}-\mu_i) \right)^2 \] が成り立つ。
\[ \sum_{p=1}^{N}(y^{(p)}-\mu_y)^2 =\sum_{p=1}^{N}(y^{(p)}-\hat{y}^{(p)})^2 +\sum_{p=1}^{N}(\hat{y}^{(p)}-\mu_y)^2 \] であり、すなわち 観測値 \(y\) のばらつきを 予測誤差\(e\) のばらつきと予測値自身\(\hat{y}\)のばらつきの 和で表すことができたことになる。 予測誤差のばらつきが小さくなればなるほど、 実測値のばらつき具合の中で予測値の占めるばらつきの度合いが大きくなり、 予測値だけで実測値のばらつきを表現できたことになる。 そこで、実測値のばらつきを\(S_{T}\)、予測誤差のばらつき\(S_E\)、予測値の分散を\(S_{R}\)とすると、 \[ S_T = S_E+S_R \] である。これより実測値のばらつきに対する予測値のばらつきの割合は
\[R^{2}=\frac{S_R}{S_T}=1-\frac{S_E}{S_T} \] の \(R^2\)を決定係数という。 決定係数が\(1\)に近いほど予測の精度は高いということを意味する。
8.4 Rによるシミュレーション
では実際に R で行ってみよう。 例として、ある確率変数 Y があり \[Y=aX+b+\epsilon\] が成り立つと仮定する。ここで、\(\epsilon\) は正規分布\(N(0,\sigma^2)\) に従うものとする。今、\(\sigma=1\) とする。\(a=2\)、\(b=3\) として乱数を発生させてみよう。
> set.seed(0)
> true_a = 2
> true_b = 3
> x1 <- runif(100)
> x2 <- rnorm(100,mean=0,sd=1)
> y1 <- true_a*x1+ true_b + x2Rには、回帰分析を行う関数として lmという関数がある。 関数の引数として目的変数と説明変数を指定する。 データフレームとして与える場合には data=データフレームの変数名 として 列、行の名前を指定する。今はベクトルデータなので 変数名を指定している。 計算結果を w に代入している。w はリストであるが、その変数名を指定すると出てきた結果を見ることができる。また、 summry() で結果の要約をみることができる。
w <- lm(y1~x1)
w
Call:
lm(formula = y1 ~ x1)
Coefficients:
(Intercept) x1
2.943 1.927 summary(w)
Call:
lm(formula = y1 ~ x1)
Residuals:
Min 1Q Median 3Q Max
-2.11900 -0.75934 0.03127 0.57068 2.52533
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.9430 0.1942 15.153 < 2e-16 ***
x1 1.9275 0.3314 5.816 7.57e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.8908 on 98 degrees of freedom
Multiple R-squared: 0.2566, Adjusted R-squared: 0.249
F-statistic: 33.82 on 1 and 98 DF, p-value: 7.574e-08\(a\)、\(b\)の推定値 \(\hat{a} =1.927\)、\(\hat{} =2.943\) 実際の値と良く一致しているように見える。 一方、決定係数は 0.25 程度と あまり良くないように見える。
図示するには、geom_point でデータを散布図として表示し、 そこにgeom_abline で直線を追加する。geom_abline()は 傾き\(a\) をslope、切片\(b\) をintercept として指定する。
> ggplot() + geom_point(aes(x=x1,y=y1) ) +
+ geom_abline(aes (intercept=w$coefficient[1],
+ slope=w$coefficient[2] ) ) 
もうひとつ正規乱数の分散を変えて行ってみよう。
> set.seed(0)
> true_a = 2
> true_b = 3
> x1 <- runif(100)
> x2 <- rnorm(100,mean=0,sd=0.1)
> y1 <- true_a*x1+ true_b + x2
> w <- lm(y1~x1)
> w
Call:
lm(formula = y1 ~ x1)
Coefficients:
(Intercept) x1
2.994 1.993 > summary(w)
Call:
lm(formula = y1 ~ x1)
Residuals:
Min 1Q Median 3Q Max
-0.211900 -0.075934 0.003127 0.057068 0.252533
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.99430 0.01942 154.17 <2e-16 ***
x1 1.99275 0.03314 60.13 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.08908 on 98 degrees of freedom
Multiple R-squared: 0.9736, Adjusted R-squared: 0.9733
F-statistic: 3615 on 1 and 98 DF, p-value: < 2.2e-16この場合、決定係数の値は0.973と高い値となっている。
8.5 まとめと展望
いくつかのデータを持っているときにそのデータが持つ特徴を線形結合によって表すのが回帰分析である。ここでは、単回帰分析を中心に係数を 求める方法について述べた。計画を立てて \(x\) の値を設定し、\(y\) の値を観測し、その\((x,y)\) のペアをもとにそのルールを知りたいとしよう。同じ観測値 \(x\) の値に対して異なる\(y\)の値が観測されれば、\(y\) の値は \(x\) だけでは決まらない のではないかと思うだろう。同じ \(x\) の値があってはならないということではないが、全てが同じ値だけでは \(y\) の値を求められないというのが \(S_{xx}\neq 0\) という条件を意味している。また、後半では係数が求まるだけではなく当てはまりの良さを考える必要があることを述べた。
参考文献
[1 ]. 日本統計学会,“統計学基礎 : 日本統計学会公式認定統計検定2級対応”, “東京図書”,2021
[2]. 金明哲,“R によるデータサイエンス(第2版)”,森北出版,2017
[3]. 中谷, 秀洋,“わけがわかる機械学習 : 現実の問題を解くために、しくみを理解する”, 技術評論社,2019
演習
- 回帰分析について述べた次の文について,誤っているものを1つ選べ。
回帰分析は目的変数を用いて説明変数を説明しようとするモデルである。
単回帰分析の場合,決定係数の値は相関係数と一致する。
回帰分析では分散共分散行列や相関行列の固有値,固有ベトルを計算して係数を求める。
解答 例として以下のように修正することができる。
回帰分析は説明変数を用いて目的変数を説明しようとするモデルである。
単回帰分析の場合,決定係数の値は相関係数の2乗と一致する。
回帰分析では分散共分散行列や相関行列の逆行列を計算する。