10 回帰分析（３）

この章では最尤法について述べ。予測誤差が正規分布に従うとした場合に最小二乗法による線形回帰と最尤法と一致することを説明する。その後ロジスティック回帰について説明する。観測されたデータを訓練用と検証用に分ける方法について述べる。

キーワード

最尤法、尤度関数、ロジスティック回帰、交差検証法

10.1 最尤法

ある観測によってデータが得られ、回帰係数が求まる。 $a=0$ と仮定して実際の値が観測される確率を求め、この値が小さいときに、滅多にないことがたまたま起こったのではなく、 $a \neq 0$ と判断するというのが帰無仮説の考え方である。

第9章では多くの正規乱数を発生させるという試行を複数回行うことでデータから導出される回帰係数の値が t分布になることを確認した。有意水準として$p=0.05$　とすることが多いが、有意水準 $0.05$ は $a=0$ と仮定しても約20回に1度は起こることをコンピュータシミュレーションで確認した。

このようなことはコンピュータシミュレーションだから行うことができるが、現実世界においては、きちんと条件を揃えた実験を何度も行うことができるとは限らない。

そこで、別の考え方を導入しよう。例えば、コイントスを$5$回行い$3$回表が出たとする。このとき、表が出る確率はいくつであると考えると良いだろうか。もし、確率が$p$であるとすると、表が3回出る確率は \[ P(F=4) = _{5}C_{3}p^3(1-p)^2 =10(p^5-2p^4+p^3) \] である。これをグラフに書くと図 Figure 10.1 のようになる。

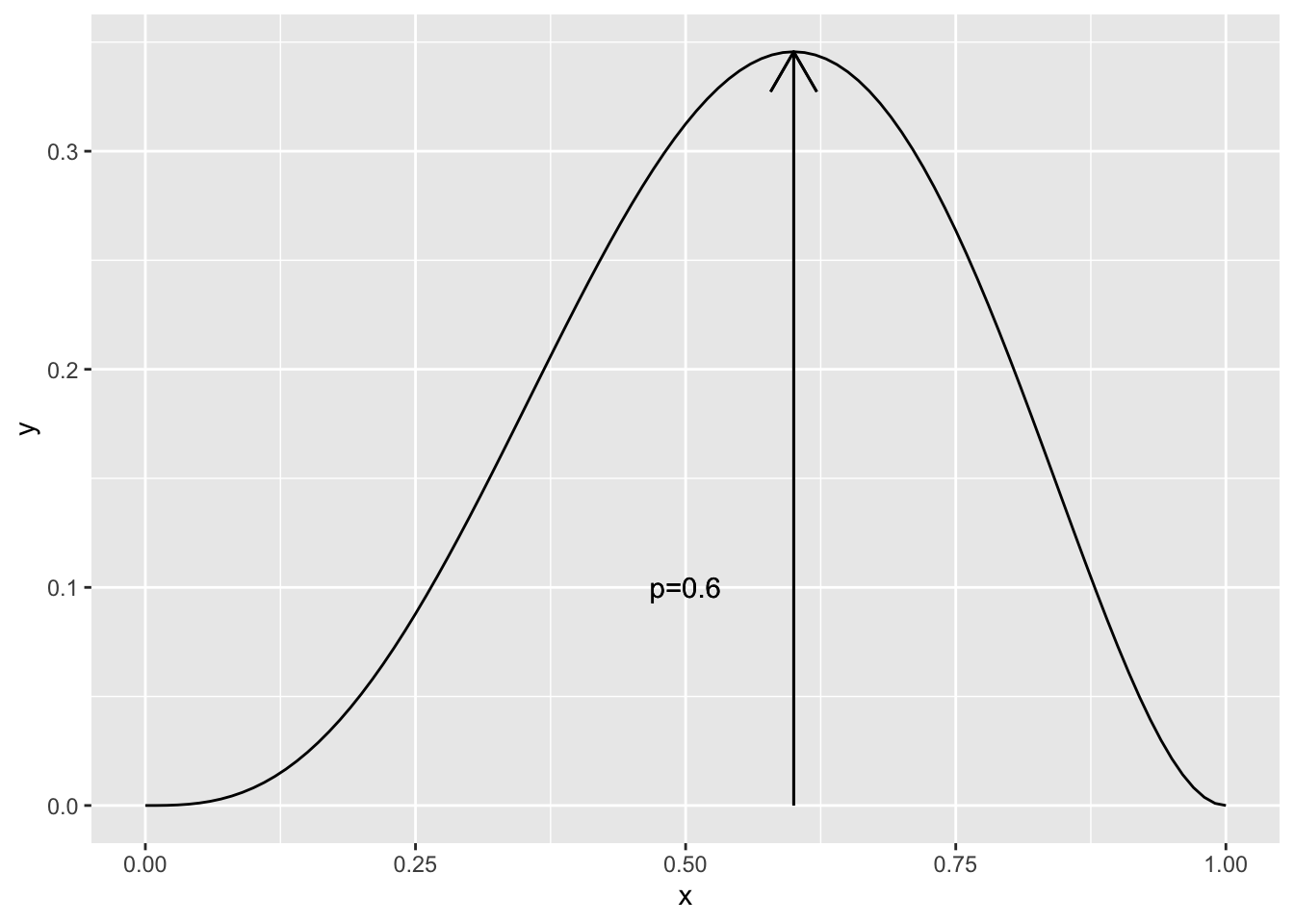
グラフでは、$p=\displaystyle\frac{3}{5}=0.6$で尤度は最大になっている。このように、今、母集団に対して確率分布を仮定し、観測されたデータを生み出す尤も（もっとも）らしさが最大となるような値を推測値とする。

これはパラメータがどんな値であれば、観測された結果が生じるのかを表す関数になっている。これを尤度関数という。結果が観測される尤もらしさが最大になるようなパラメータを求める。これによって推測されるパラメータを最尤推定量という。

線形回帰について考えてみよう。 $N$ 組のデータ $(x^{(i)},y^{(i)})$ があるとする。今、 $Y=a X +b+\epsilon$ が成り立つかどうかを調べる。ここで、$$ は平均$0$、分散 $\sigma^2$ に正規分布に従うとする。すると、ある$x^{(i)}$ の時に値が $y^{(i)}$ になる確率は $y^{(i)} - (ax^{(i)}+b)$ が平均$0$、分散 $\sigma^2$ の正規分布に従うとして、

\[\begin{eqnarray} p^{(i)}&=& \frac{1}{\sqrt{2\pi}\sigma} \exp \left( -\frac{\left(y^{(i)}-(ax^{(i)}+b)\right)^2}{2\sigma^2} \right) \end{eqnarray}\]

となる。各回が独立と考えると、$N$個の観測値が求まる確率密度は $p^{(i)}$ の積によって

\[\begin{eqnarray} L(a,b) &=& p^{(1)}p^{(2)}\cdots p^{(N)}= \prod_{i=1}^N p^{(i)} \end{eqnarray}\]

となるので、この値が最大になる $a$、$b$ を求めることになる。そのために、この自然対数 $\log_{e}f(x)$ を考えよう。また、$x<1$ で$\log$は負になるので $-1$倍して $-\log L(a,b)$を考える。自然対数$y=\log x$ は $x$ が増加すれば $y$ も単調に増加する関数なので、$L(a,b)$が最大になるとき、 $-\log L(a,b)$ は最小になる。これを計算すると

\[\begin{eqnarray} -\log L(a,b) &=& \log \prod_{i=1}^N p^{(i)} \\ \nonumber &=& -\sum_{i=1}^N \log p^{(i)} \\ \nonumber &=& - \sum_{i=1}^N \log \left( \frac{1}{\sqrt{2\pi}\sigma} \exp \left( -\frac{\left( y^{(i)}-(ax^{(i)}+b) \right) ^2 }{2\sigma^2} \right) \right) \\ \nonumber &=& \sum_{i=1}^N \left( \log \sqrt{2\pi}\sigma - \log \exp \left( -\frac{\left( y^{(i)}-(ax^{(i)}+b) \right)^2 }{2\sigma^2} \right) \right) \\ &=& {N}\log \sqrt{2\pi}\sigma + \frac{1} {2\sigma^2} \sum_{i}^{N} \left( (y^{(i)}-(ax^{(i)}+b) \right)^2 \end{eqnarray}\]

となる。これより、 \[ \sum_{i}^N \left( (y^{(i)}-(ax^{(i)}+b) \right)^2 \] が最小になるような $a$、$b$を求めることになる。このように、予測誤差が正規分布に従うとすると最尤法と最小二乗法とで推定値は一致する。

この章の最初の例では lmによる回帰分析行った。その結果のリストにはresiduals で残差がある。このヒストグラムを見てみよう。

> ggplot()+
+   geom_histogram(aes(x=w$residuals,
+                      y=after_stat(density)),bins=15)

これを見ると正規分布に近い形をしている。この他に誤差が正規分布になっているかどうかを見るための方法として Q-Q プロットというものがある。正規分布に従うサンプルサイズ $N$個のデータがあるとし、これが小さい順に整列しているものとする。データの $i$番目の値と正規分布の$i$番目までの分位点となる$x$座標と比較する。

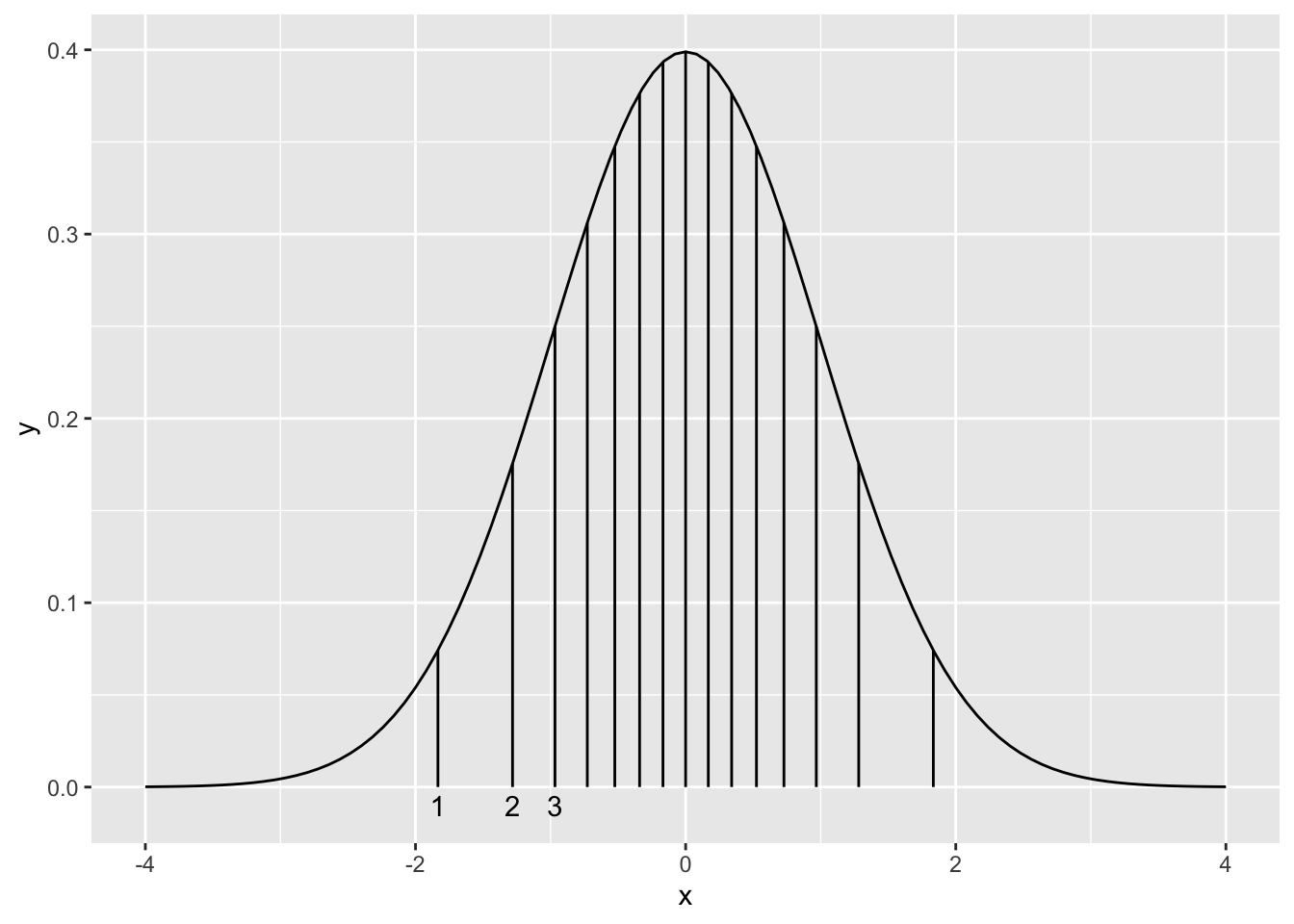
この $i$ 番目の$x$座標は累積正規分布の$y$座標を等間隔に $N$等分したときの下から $i$番目の点の $x$座標であり、 qnorm() という関数で求めることができる。

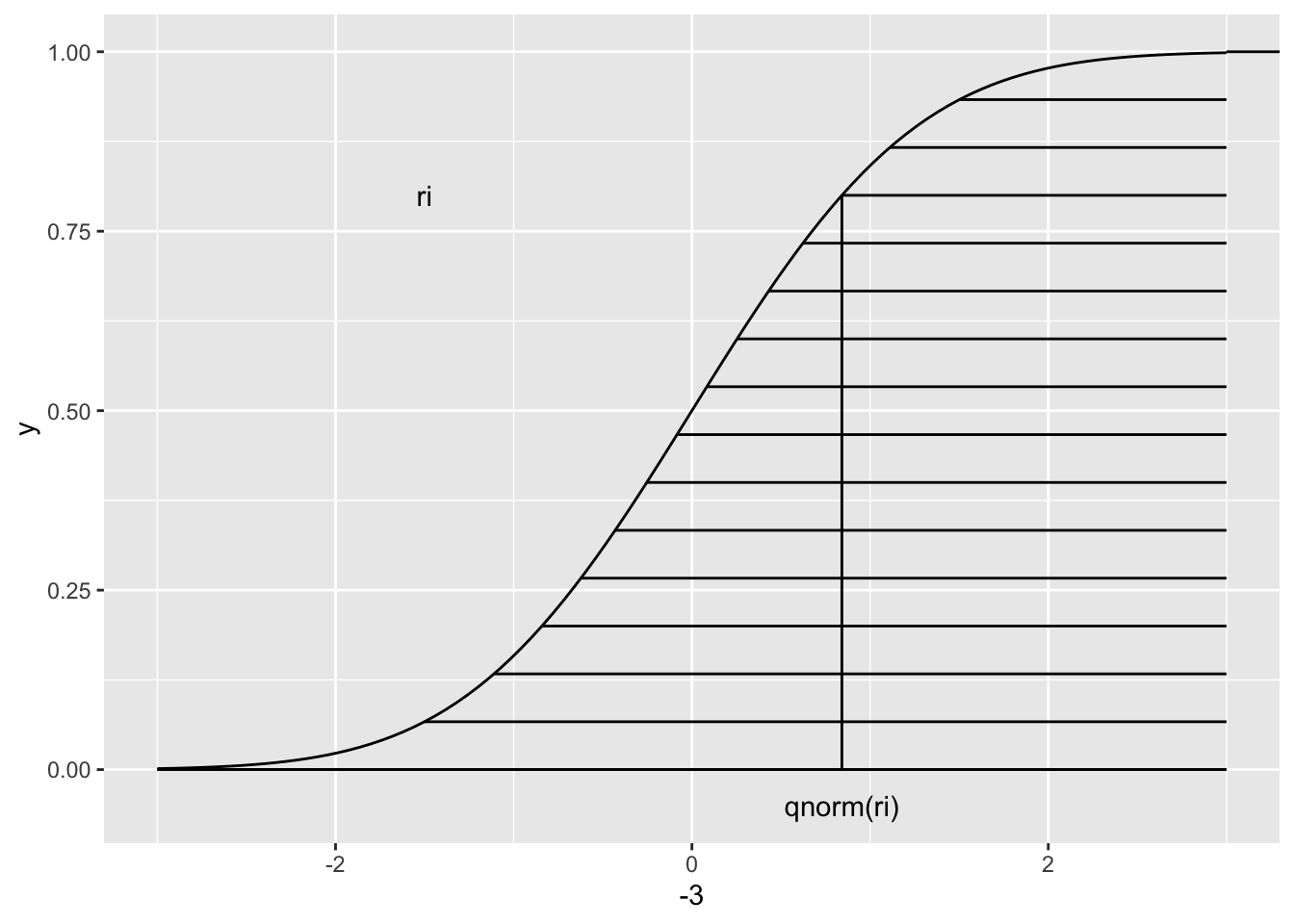
Q-Q プロットは上記のようにして求めた $x$座標と元のデータを $y$座標にして比較した散布図である。データが平均$\mu$、分散$\sigma^2$ の正規分布に従っているとすると、$y=\sigma x + \mu$ 上にのる。

ggplot ではgeom_qq()とすると、Q-Q プロットの散布図を描き、geom_gg_line()` で直線を引く。

> ggplot(mapping=aes(sample=w$residuals))+
+   geom_qq()+
+   geom_qq_line()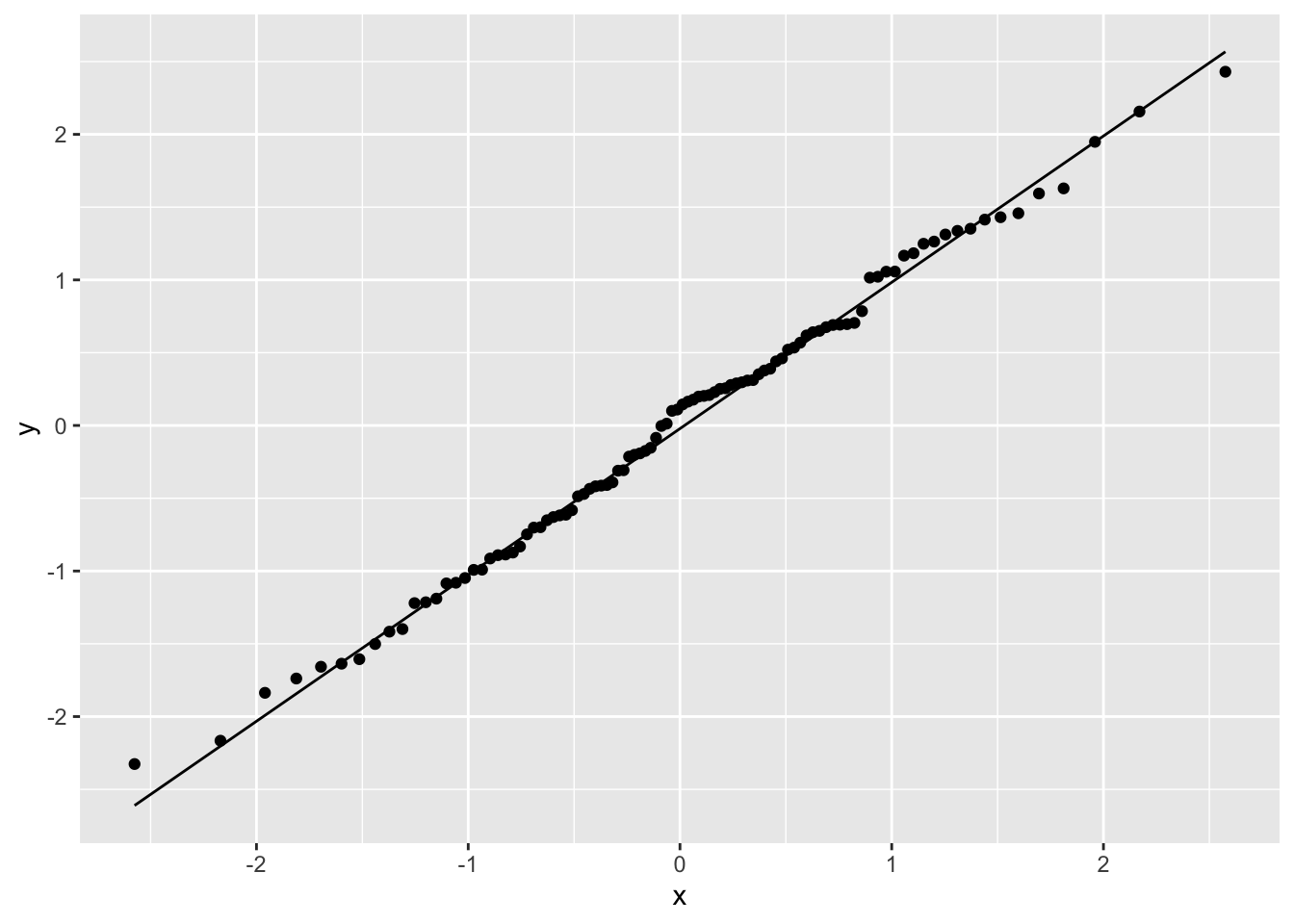

$x$座標を求めてみよう。 Rではデータ数が$N$ とすると $i$ 番目の $y$座標は

\[\begin{eqnarray} y_i &=& \frac{ i - a }{N+ 1- 2a} \end{eqnarray}\]

として計算している。$a$ は $N \leqq 10$ の時 $\frac{3}{8}$、それより大きい時は $\frac{1}{2}$ である。 $x$ 座標は qnorm で求められる。データが整列されているとは限らない。 Rでは rank()という関数があり、小さい順の順位を返す。もし同じ値があった場合には、順位を平均する。

> x <- c(6,2,8,8,4)
> rank(x)

[1] 3.0 1.0 4.5 4.5 2.0

これを用いると $x$座標は

> x <-  ( ( rank(w$residuals) - 0.5) / length(w$residuals) ) %>%
+   qnorm()
> head(x)

          1           2           3           4           5 
 0.06270678  0.53883603 -1.81191067 -2.17009038  1.10306256 
          6 
 1.43953147

として求めることができる。

10.2 ロジスティック回帰

ある授業を履修する。その授業の単位を取ることと放送授業をどれだけ閲覧するかの関係を知りたいとしよう。ネット配信であれば、サーバにログが残り、それぞれの学生の閲覧時間が集計できる。おそらく放送授業を見た方が単位を取る確率は高くなると思われる。確率は高くても偶然失敗してしまうこともある。放送授業を全く見なければ単位を取る確率は低くなる。それでも合格することもあるかもしれない。観察を通して得られるデータは閲覧時間と単位を取得したかどうかであり、この確率にあたるものを想像することはできない。次の例はこのような状況をモデル化したものである。実際に行う場合はや b を変更して試してほしい。

> set.seed(100)
> N <- 250 
> xmin <- 0
> xmax<- 10
> x<- runif(N,xmin,xmax)
> a <- -10
> b <- 2
> p <-  exp(a+b*x) / ( 1+exp(a + b*x) )
> y <- vector("numeric",length=N)
> for(i in 1:N){
+   y[i] <- rbinom(1,size=1,prob=p[i])
+ }
> train <- tibble(x=x,y=y)
> ggplot(data=train,aes(x=x,y=y))+geom_point()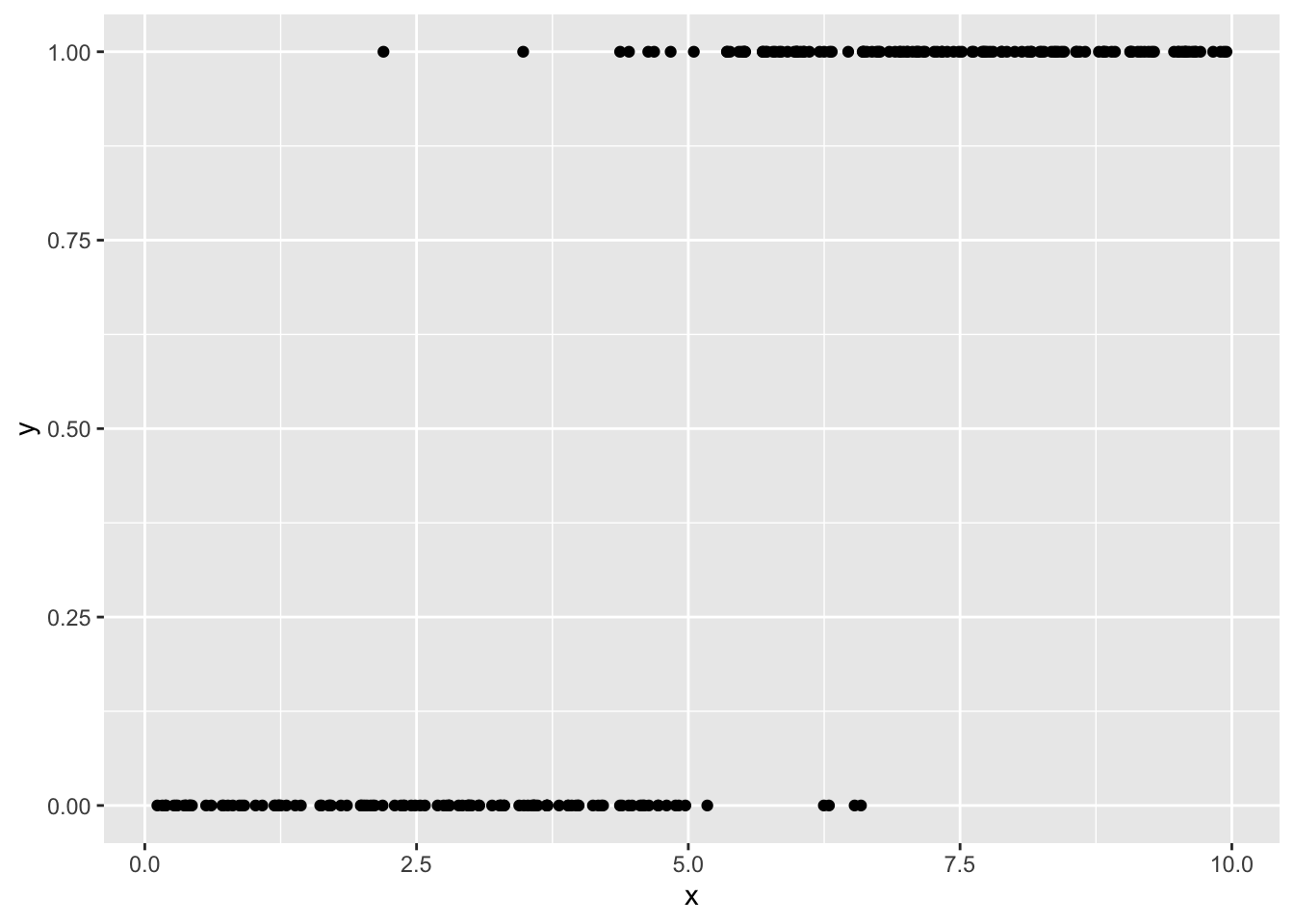

ある事象が起こる確率を$p$ とするとき、その事象が起こらない確率$1-p$ との比$\frac{p}{1-p}$ をオッズ といい、この対数をとった値 $\log\left( \frac{p}{1-p} \right)$を ロジット という。このロジットについて

\[\begin{eqnarray} \log\left( \frac{p}{1-p} \right) &=& a_0 +a_1 x_1 +a_2 x_2+\cdots + a_n x_n \end{eqnarray}\]

で表されるモデルをロジスティック回帰という。 $\log\left( \frac{p}{1-p} \right)=x$ とすると

\[\begin{eqnarray} p &=& \frac{\exp(x)}{1+\exp(x)} = \frac{1}{1+\exp(-x)} \end{eqnarray}\]

となる。先ほどの図の例は一変数のロジスティック回帰となる。

\[\begin{eqnarray} \nonumber p &=& \frac{\exp(a+bx)}{1+\exp(a+bx)} \end{eqnarray}\]

$a$、$b$ を変えて図を書くと次のようになる。

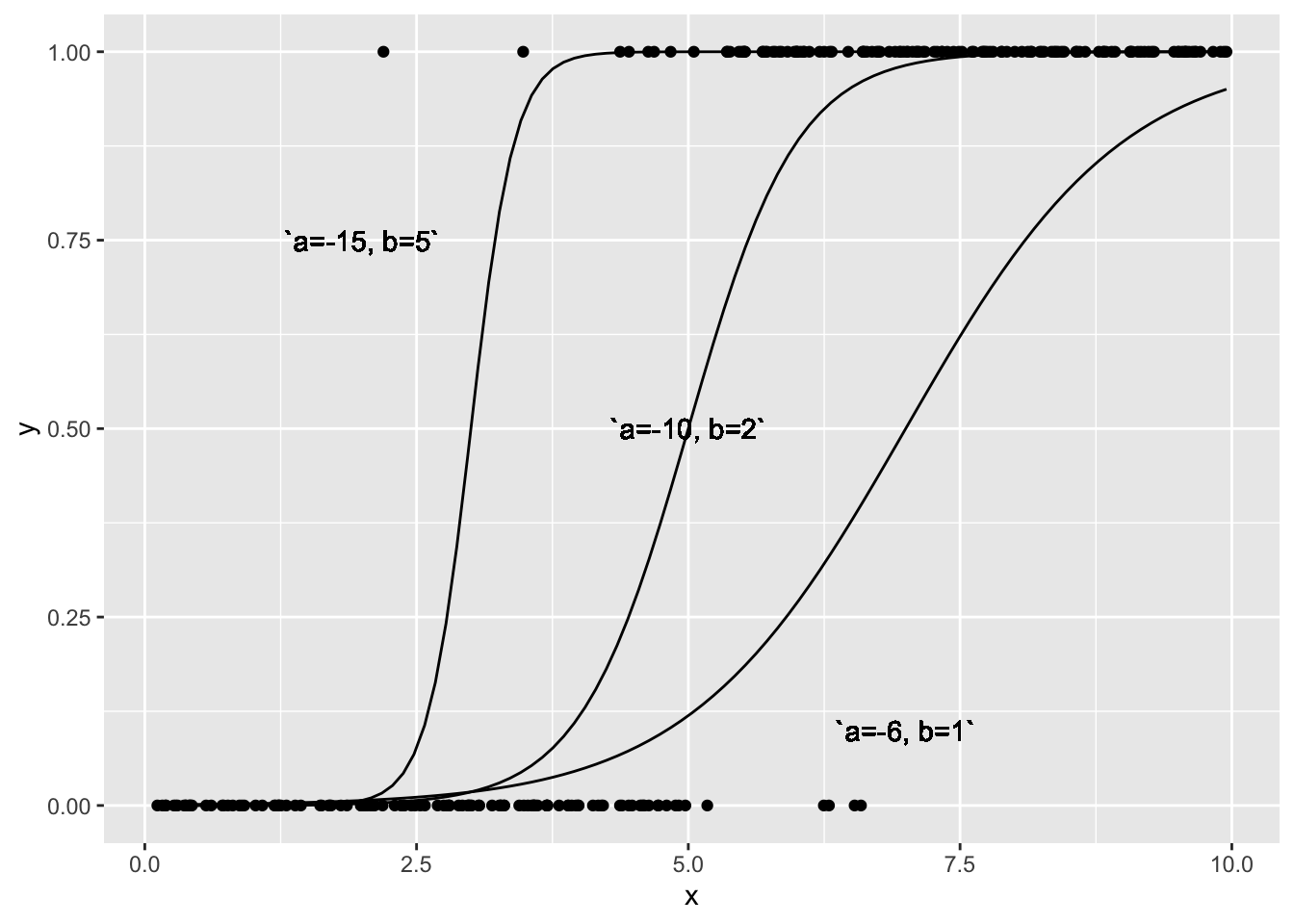
この$a$、$b$を最尤法を用いて解いてみよう。Rで最尤法を用いるには glm という関数を用いる。glm では確率分布

> b_lm1 <- glm(y~x,data=train,family=binomial)
> b_lm1


Call:  glm(formula = y ~ x, family = binomial, data = train)

Coefficients:
(Intercept)            x  
     -9.522        1.899  

Degrees of Freedom: 249 Total (i.e. Null);  248 Residual
Null Deviance:      346.5 
Residual Deviance: 86.15    AIC: 90.15

真の値に近い値を推定していることが見て取れる。最尤推定では大数尤度と予測に用いいたパラメータ数からAIC情報量基準(Akaike’s Information Criteria)が計算され、これが最小となるモデルを選ぶ。たとえば、今回の例では y~x の代わりにy~1($a=0$ を想定したモデル)や y~x-1($b=0$ としたモデル)と比較してみることができる。結果から確率を予測するには predict を利用することができる。使う確率分布によって、出力のtype が異なり、二項分布の場合には response とすると確率を求めてくれる。

> M <- 200
> test <- tibble(x = seq(xmin,xmax,(xmax-xmin)/(M+1) ) )
> y <- predict(b_lm1, newdata=test, type="response" )
> test <- test %>% mutate(y=y)
> ggplot(data=train,aes(x=x,y=y))+geom_point()+
+   geom_point(data=test,aes(x=x,y=y),size=0.1)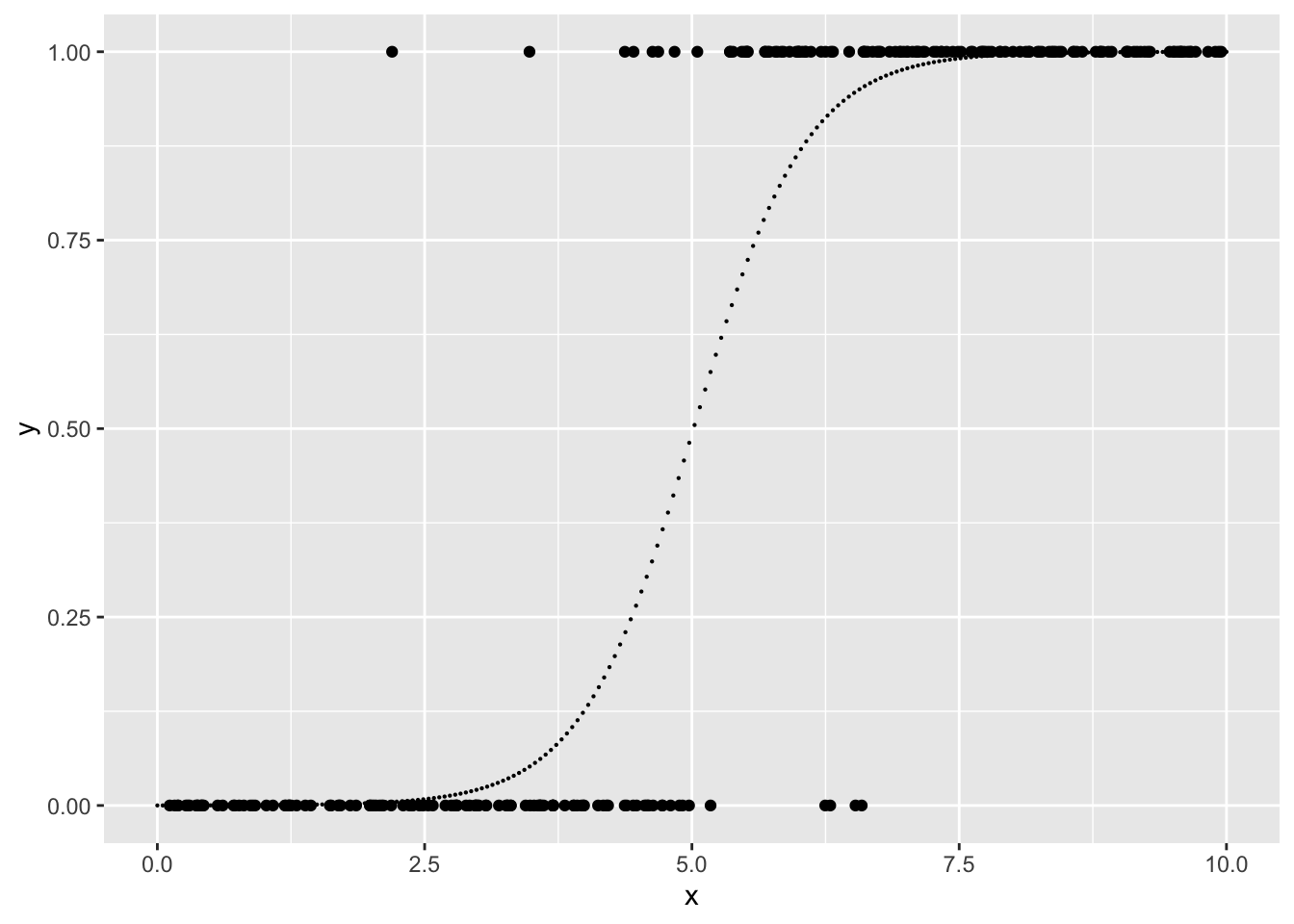

10.3 サンプル抽出

今までは乱数を発生させて繰り返し計算するということをしてきたが、現実の世界では同じことを繰り返して観察することができないことも多い。そして限られた回数のデータをもとサンプルから予測を行い、その精度を評価する。そのためには回帰係数を求めるといった予測器を生成するための訓練(training )用のデータと、その精度を評価するための検証（validation）用のデータが必要となる。データ数が多ければ、7割3割といった割合で分ければ良い。これをホールドアウト法(hold-out法)という。また、データ数を$k$個に分割し、そのうちの $k-1$ 個を訓練用に $1$ 個を検証用にする。ここで、検証を$k$回繰り返した検証結果を平均して評価するという方法もある。これをk交差検証法（k-cross validation）という。 $k$ 回の検証を行うことで、どのデータも訓練、検証の両方に用いられることになる。 irisは R にあらかじめインストールされているデータセットで、あやめの花のデータである。３種類の種があり、がく片（Sepal）の幅と長さ花びら（Petal）の幅と長さのデータが与えられている。外見の特徴から種を分類する例などに用いられる。

> head(iris)

  Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1          5.1         3.5          1.4         0.2  setosa
2          4.9         3.0          1.4         0.2  setosa
3          4.7         3.2          1.3         0.2  setosa
4          4.6         3.1          1.5         0.2  setosa
5          5.0         3.6          1.4         0.2  setosa
6          5.4         3.9          1.7         0.4  setosa

> nrow(iris)

[1] 150

R でこのデータを訓練用と検証用に分ける方法を考える。データ数は150行で50個ごとに同じ種が続いている。ランダムに 120個抽出したい。有限個の要素の中からランダムに抽出する関数として R には sample という関数がある。要素抽出には、「カードを引いても戻さない」ような非復元抽出と「コインを繰り返しトスする」ような復元抽出の２種類がある。何も指定しないと非復元抽出になる。非復元抽出は戻さないので指定したデータの個数以上の抽出はできない。

> set.seed(0)
> x <- sample(1:150,120)

復元抽出は replace=TRUEとする。また、prob で確率分布を指定できる。

次の例は表と裏が等間隔でない場合のコイントスを100回行って回数を数えたものである。

> set.seed(64)
> sample(1:2,100,replace=TRUE,prob=c(2/5,3/5)) %>% table()

.
 1  2 
51 49

iris はデータフレーム形式をしているので、先ほど抽出した x の行だけ取り出したものを訓練用にして、それ以外の行を検証用にする。

> train <- iris[x,]
> test <- iris[-x,]

次に $5$個のグループに分けることを考えよう。一つのグループに入る個数は30個。$1$ から$5$を30個作り、 $150$個の要素から非復元抽出でランダムに全て取り出すことをすれば全部の要素にランダムにグループ番号を割り当てることができる。 a==1とすると値が1の行だけTRUEになるので、iris[a==1,]とするとこの操作で 1のグループに割り当てられた行のみ抽出することになる。

> a <- rep(1:5,each=30)
> a <- sample(a)
> iris[a == 1, ] %>% head()

   Sepal.Length Sepal.Width Petal.Length Petal.Width
9           4.4         2.9          1.4         0.2
15          5.8         4.0          1.2         0.2
18          5.1         3.5          1.4         0.3
23          4.6         3.6          1.0         0.2
32          5.4         3.4          1.5         0.4
38          4.9         3.6          1.4         0.1
   Species
9   setosa
15  setosa
18  setosa
23  setosa
32  setosa
38  setosa

for文を使うと繰り返し行うことができる。

> for(i in 1:5){
+   train <- iris[a != i,]
+   test <- iris[a == i,]
+ }

10.4 まとめと展望

1変数の回帰分析から変数を増やした最小２乗法による回帰分析について説明し、最後に最尤推定について述べた。二項分布の例ではを示したが、現実の世界では理想的な二項分布に限らず、観測されたデータをもとに分布を推定するベイズ統計を用いる方法もある。そこへの展開は参考文献の[1] がよく知られている。一般化線形回帰については [2] がある。 R でベイズ統計を行う方法を説明する本として [3] がある。

参考文献

[1]. C. M. Bishop, 元田浩, 栗田多喜夫,樋口知之,松本裕治,村田昇, “パターン認識と機械学習 : ベイズ理論による統計的予測（上下）”,丸善出版,2012

[2]. 久保拓弥,“データ解析のための統計モデリング入門 :一般化線形モデル・階層ベイズモデル・MCMC”, 岩波書店,2012,

[3]. 馬場真哉,“RとStanではじめるベイズ統計モデリングによるデータ分析入門”, 講談社,2019

演習

パイプ処理を行い、スクリプトを残しておけば変数を減らすことができる。紙面を減らす意味で、あえて文字数を減らしているが、本来変数を設定するのであれば、どういう変数かが後からわかるようにしておく方がよい。特に関数は後から使うことが多いので、名前自体がすぐ思い出せた方が良い。変数名が長くても、R では補完機能があるので、途中までタイプした後にタブキーを押せば候補が表示されるか、候補が1つならば最後まで補完される。 k 交差検証法では別のa という変数を設定したが、グループもデータフレームの列にするという方法もある。データセットを同じ名前で変形するのは気が引けるので別名にしておくと、次のように抽出することができる。

> a <- rep(1:5,each=30)
> a <- sample(a)
> df_iris <- iris %>% 
+   mutate(group =sample( rep(1:5,each=30) ) ) 
> df_iris %>% filter(group !=1) %>% head()

  Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1          5.1         3.5          1.4         0.2  setosa
2          4.7         3.2          1.3         0.2  setosa
3          4.6         3.1          1.5         0.2  setosa
4          5.0         3.6          1.4         0.2  setosa
5          5.4         3.9          1.7         0.4  setosa
6          4.6         3.4          1.4         0.3  setosa
  group
1     2
2     5
3     5
4     3
5     4
6     3