6 アソシエーション分析

2種類のデータ間の関係を調べる方法として相関係数や共分散があるが、これらは関係の強さを調べるものであり、どちらがもう一方に影響を与えているかという因果関係を調べるものではない。そこで、データから「 \(A\) ならば\(B\)である」という関係を抽出するアソシエーション分析 (Association Analysis)について扱う。

キーワード

支持度、信頼度、期待信頼度、リフト値

6.1 POSシステム

近年、店舗で商品を販売する際には商品の情報をあらかじめコンピュータに登録し、売り上げや在庫の情報を管理できるようになった。これによって、正確な在庫管理ができるだけでなく、どういった商品がどういった時に売れているのかといった販売記録などの情報を入手できるようになった。このようなシステムを POSシステム(Point of Sales System、ポスシステム) という。マーケティングにおけるデータ活用の話として、スーパマーケットでの「紙おむつ」の話がある。あるスーパーマーケットで客の購入履歴を調べたところ、週末の夕方になると、「紙おむつ」を買った人の中で、同時に「ビール」を買っている人が多いという特徴のことであった。そして、この話は、POSシステムによって購買データのすべてのデータを扱うことができるようになり、大量の種類の商品の組み合わせを調べてみた結果、興味深いルールを拾い出すことができたということである。この点で、限られたサンプルを用いた標本調査とは違う特徴がある。

6.2 アソシエーションルール

先ほどの例において、「紙おむつを買う」、「ビールを買う」といった事象について考える。「紙おむつを買う」という事象を \(A\) 、「ビールを買う」という事象を \(B\) として、「紙おむつを買う人はビールも買う」ということを \(A \Rightarrow B\) (\(A\) ならば \(B\))と書く。例えば、「ビールを買う人は紙おむつも同時に買う」ということを表したいのであれば、 \(B \Rightarrow A\) と書く。このような条件文のことを アソシエーションルール (association rule 連関規則)という[^arules-1]。 アソシエーション分析とは、起こりうる様々なルールの中から有用なルールを抽出する手法のことをいう。アソシエーション分析は、買い物かごの分析ということで バスケット分析 ともいう。ここで条件式について考えるために、別の例として、「横浜市民である」という事象( \(A\) )と「神奈川県民である」という事象( \(B\) )について考えてみよう。この場合、横浜市民であれば、神奈川県民であるからルール \(A \Rightarrow B\)　は成り立っている。しかし、神奈川県民であっても、川崎市や相模原市に住んでいるかもしれないので、必ずしも \(B \Rightarrow A\) が成り立つとは限らない。「紙おむつ」の例でいうと、「ビールを買った人が紙おむつを買うことが多い」ということと「紙おむつを買った人がビールを買うことが多い」ということとは意味が違う。このように、矢印の向きは大きな意味を持っている。そこで、このルール \(A \Rightarrow B\) において、 \(A\) を条件部 (rule head ルールヘッド)といい、 \(B\) を結論部 (rule body ルールボディ)という。こうしたルールを抽出するために、いくつかの量を定義しよう。様々な購買記録などにおいて、\(A\) が起こった回数をすべてカウントし、この回数を \(n(A)\) と書く。同様に \(B\) という事象が起こった回数を \(n(B)\) とする。そして、すべての事象\(\Omega\)の回数を \(n(\Omega)\) としよう。そして、\(A\) と \(B\) が同時に起こる事象回数、先ほどの例でいえば、「紙おむつとビールを両方買う」事象の起きた回数を \(n(A,B)\) と書く。アソシエーション分析ではこの値をもとに次の 4つの値をそれぞれ計算する。このように判断基準として用いる値を指標という。

期待信頼度(expected confidence)： Bが起こる確率

\[\begin{eqnarray} p(B) &=& \frac{n(B)}{ n(\Omega) } \end{eqnarray}\]

支持度(support)： A と B が共に起こる確率

\[\begin{eqnarray} p(A,B) &=& \frac{n(A, B)}{ n(\Omega)} \end{eqnarray}\]

信頼度(confidence)： A が起こった前提で、Bが起こる確率

\[\begin{eqnarray} p(B|A) &=& \frac{n(A,B)}{n(A)} \\ &=& \frac{p(A,B)}{p(A)} \end{eqnarray}\]

リフト値(lift)：信頼度を B が起こる確率で割ったもの。

\[\begin{eqnarray} \frac{p(B|A)}{p(B)} &=& \frac{p(A,B)}{p(A)p(B)} \end{eqnarray}\]

今、\(A \Rightarrow B\)という条件について考える。さらに、複数の商品を購入する場合について考えてみよう。例えば、\(A\)を{紙おむつ、ポテトチップス}を買った場合、\(B\)を{ビール}を買った場合であるとする。このとき、\(A\) と\(B\) がともに起こるとは、{紙おむつ、ポテトチップス、ビール}を買っているという場合のことを意味する。では、複数のアイテムとして、\(A\)として{紙おむつ、ポテトチップス}、\(B\) として{ビール、ポテトチップス} といったことを考えてみよう。この場合、\(A\) と\(B\) が同時に起こるというのは、「紙おむつとポテトチップス」を買っていて、なおかつ「ビールとポテトチップス」も買っているという場合である。これを図で書くと図(Figure 6.1) のように表すことができる。

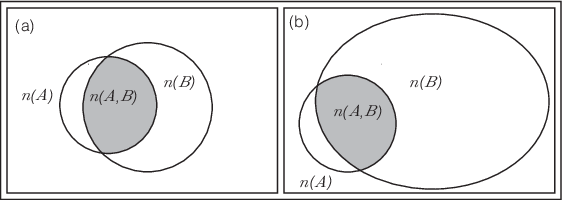
図(Figure 6.1) において、次のような状況を考えてみよう。この図が (a)や(b)という店で \(A\){ガム}、\(B\){飴}を買う人の数を表しているとしよう。これについて、 \(A \Rightarrow B\) というケースについて考えてみよう。

	(a)		(b)
\(n(\Omega)\)	100	\(n(\Omega)\)	100
\(n(A)\)	25	\(n(A)\)	25
\(n(B)\)	40	\(n(B)\)	80
\(n(A,B)\)	20	\(n(A,B)\)	20

このとき、それぞれの値を計算すると、

(a): \[\begin{aligned} \mbox{支持度}=\frac{20}{100}=0.2&\mbox{,}& \mbox{期待信頼度}=\frac{40}{100}=0.4 \\ \mbox{信頼度}=\frac{20}{25}=0.8 &\mbox{,}& \mbox{リフト値}=\frac{0.8}{0.4}=2 \end{aligned}\]
(b): \[\begin{aligned} \mbox{支持度}=\frac{20}{100}=0.2 &\mbox{,}&\mbox{期待信頼度}=\frac{80}{100}=0.8 \\ \mbox{信頼度}=\frac{20}{25}=0.8&\mbox{,}&\mbox{リフト値}=\frac{0.8}{0.8}=1 \end{aligned}\]

このように、どちらのケースも信頼度はかなり高い値になっており、ガムを買った人は同時に飴も買う確率が高い。しかし、(b)のケースではもともと飴を買う確率が高く、結果的にガムを買った人がついでに飴を買っていると考えることができる。一方、(a)のケースではガムを買った人が飴を買う確率(\(0.8\))は、ただ飴を買う確率(\(0.4\))よりも大きい。すなわち、ガムを買った人は特に飴を買うという傾向があるということが分かる。リフト値についてもう一つの例を考えてみよう。宝くじが当たると評判の売り場があるとしよう。その評判が本当かどうかを確認したいとする。ここで、\(A\)がその評判の売り場で宝くじを買うという事象、\(B\)は宝くじが当たる事象であるとしよう。今、知りたいのはその店が特によく当たるのかどうかということである。このとき、\(p(B)\)はどの店でもよいので宝くじが当たる確率で、\(p(B|A)\)はその売り場で宝くじが当たる確率である。したがって、リフト値が\(1\)より高いということは、その売り場で買う方が通常の当たる確率よりも高いと考えることができる。後に述べる例のように、店で扱う商品の数が増えると購入される商品の組み合わせも多様になり、信頼度の値自体は小さくなる。したがって、支持度や信頼度の値がいくつだから意味があると判断できないことがある。その場合にはリフト値が1より大きいということが 1つの基準になる。

6.3 Rによるシミュレーション

ではこれをRにて計算してみよう。シミュレーションには、arulesというパッケージの中にあるaprioriという関数を用いる。これはアグラワル(R. Agrawal)ら（参考文献[1]）によって提案されたアプリオリというアルゴリズムに基づいた関数である。先ほどは「\(A\)ならば\(B\)である」というルールに関して、どのような指標を調べるのかということについて説明した。このように、１つ１つの指標の計算自体は単純であった。しかし、アソシエーション分析では、あらかじめ調べたいルールが分かっているというわけではない。多くのアイテムの組み合わせについて調べてみて、その中から意味のあるルールを抽出しようとするのである。そのため調べる組み合わせの数は非常に多くなってしまう。例えば飲み物のみを扱っている店を考えてみよう。このとき、調べた結果、「コーヒー」と「紅茶」の両方を買っている人が同時に「烏龍茶」を買っている、というように複数のアイテムの組み合わせからなるルールに意味があるということが起こるかもしれない。このように、まずは調べる段階では複数の商品からなる組み合わせもすべて考慮に入れて調べる必要があるだろう。そこで、アプリオリではまず支持度に着目し、この値が基準よりも小さいものを無視することで調べる集合の組み合わせを減らそうという工夫を行う。例えば、「\(A\)ならば \(B\) である」というルールについて考えてみよう。このとき、支持度というのは \(A\)と\(B\)が同時に起こる確率のことを意味していた。したがって、支持度が小さいということは、「\(A\) ならば\(B\)である」という状況が起こることはとても少ないということを意味している。このように支持度が小さいということはあまり起きない事柄であり、ルールとして意味があったとしても、影響があまりないルールであると考えることができる。また、「コーヒー」を買っている人が「紅茶」を買うかどうかということを考えてみよう。このとき、支持度が小さいということは、「コーヒー」と「紅茶」を同時に買うということが非常に少ないということである。そうであれば、「コーヒー」と「紅茶」と、さらに「烏龍茶」という3つの商品を同時に購入するケースはさらに起こりにくいと考えることができる。その結果、「コーヒー」と「紅茶」を含む3つ以上の商品の組み合わせについては無視することができる。このように、最初に支持度の最小値を設定し、それよりも割合の小さな組み合わせの集合を無視することにすれば、あるアイテムの組み合わせが無視できるとき、その組み合わせにさらに他のアイテムを組み合わせた集合も無視できるとことになり、結果的に計算の手順を減らすことができる。このように、アプリオリは、よく起こるアイテムの組み合わせをすべて調べるために、最小の支持度を設定し、まずその値よりも小さい、めったに起きない組み合わせのみ除外して考える。そのもとで次にある値以上の信頼度について、意味のあるルールを探すということをする。では、実際に使ってみよう。初めて使う場合には、arulesというパッケージをインストールする必要がある。インストールされていたら、パッケージを使うために読み出す。すると次のように表示される。

> library(arules)

 要求されたパッケージ Matrix をロード中です


 次のパッケージを付け加えます: 'arules'

 以下のオブジェクトは 'package:base' からマスクされています:

    abbreviate, write

今回は主に、inspect()、apriori()、itemFrequency()、sort() といった関数を使う。また、データとしては、arulesのパッケージに付随したデータである Groceries を使うことにする（@hasler）。以降Groceries は長いので g0 とする。

> data(Groceries)
> g0 <- Groceries
> g0

transactions in sparse format with
 9835 transactions (rows) and
 169 items (columns)

データは各行がその時の購入品の集合になっているこれを見ると\(169\)種類の商品で、9835回の取引（トランザクション：transaction)を表す。 R では asという型を変形する関数がある。最初の数行を見ると

> g0 %>% head() %>% as("data.frame")

                                                                  items
1              {citrus fruit,semi-finished bread,margarine,ready soups}
2                                        {tropical fruit,yogurt,coffee}
3                                                          {whole milk}
4                         {pip fruit,yogurt,cream cheese ,meat spreads}
5 {other vegetables,whole milk,condensed milk,long life bakery product}
6                      {whole milk,butter,yogurt,rice,abrasive cleaner}

すべてのアイテムを列に並べた行列形式にすると、各回の取引で購入する商品の数はそれほど多くないので、行列はほとんどの成分が \(0\) の行列である。このような行列を疎(またはスパース、sparse)であるという。

> g0 %>% head() %>% as("matrix")

CSVの形式にして書き出すには write() という関数がある。

> g0 %>% write("g0.csv",sep=",")

この取引データからルールを抽出するには apriori() という関数を実行する。

> grules <- apriori(g0)

Apriori

Parameter specification:
 confidence minval smax arem  aval originalSupport maxtime support minlen
        0.8    0.1    1 none FALSE            TRUE       5     0.1      1
 maxlen target  ext
     10  rules TRUE

Algorithmic control:
 filter tree heap memopt load sort verbose
    0.1 TRUE TRUE  FALSE TRUE    2    TRUE

Absolute minimum support count: 983 

set item appearances ...[0 item(s)] done [0.00s].
set transactions ...[169 item(s), 9835 transaction(s)] done [0.00s].
sorting and recoding items ... [8 item(s)] done [0.00s].
creating transaction tree ... done [0.00s].
checking subsets of size 1 2 done [0.00s].
writing ... [0 rule(s)] done [0.00s].
creating S4 object  ... done [0.00s].

すると、ルールを求める計算が行われる。この結果を見ると、writing... で 0 rules となっている。関数apriori() はオプションで多くのパラメータを設定することができる。何も指定しない場合省略時の既定値で計算する。信頼値(confidence) が \(0.8\)以上、支持度(support) \(0.1\)以上のものを調べることになっている。支持度が \(0.1\) 以上ということは、 10回に1回以上購入されることがあるということを意味する。また、信頼値が \(0.8\) とは、ある商品を買ったときに、 10回に8回以上はセットで購入される品ということである。今回はそうした条件で調べた所、ルールが見つからなかったという結果になった。こうした値を適切に設定するには、データの特徴を把握する必要があるが、まずは、aprioriの使い方を知るために、最低支持度や最低信頼度の値を変えてシミュレーションしてみよう。支持度や信頼度の値を指定するためには、parameter=list()として値を設定する。とする。parameter は p=list()と省略して書くこともできる。

> grules2 <- apriori(g0,p=list(support=0.01,confidence=0.5))

Apriori

Parameter specification:
 confidence minval smax arem  aval originalSupport maxtime support minlen
        0.5    0.1    1 none FALSE            TRUE       5    0.01      1
 maxlen target  ext
     10  rules TRUE

Algorithmic control:
 filter tree heap memopt load sort verbose
    0.1 TRUE TRUE  FALSE TRUE    2    TRUE

Absolute minimum support count: 98 

set item appearances ...[0 item(s)] done [0.00s].
set transactions ...[169 item(s), 9835 transaction(s)] done [0.00s].
sorting and recoding items ... [88 item(s)] done [0.00s].
creating transaction tree ... done [0.00s].
checking subsets of size 1 2 3 4 done [0.00s].
writing ... [15 rule(s)] done [0.00s].
creating S4 object  ... done [0.00s].

parameter specification:の部分にはconfidenceと supportの値がそれぞれ指定した値になっていることを確認しよう。 writing ...を見るとport 値が \(15\)個のルールがあったことを意味している。抽出されたルールを実際にみるためには、inspect()というコマンドを用いる。生成されたルールが多くある場合には、inspect()ですべてのルールを表示すると見づらいので、先頭からの数行を表示する head() という関数と、並び替えを行う sort() という関数を組み合わせて利用する。ここで、sort()という関数には、 Rの基本セットに含まれる関数とarulesというパッケージで追加された 2種類の関数があり、どちらも同じ名前をしている。引数がトランザクションデータやアイテム集合の場合には、 R の方で自動的に判断して、arulesというライブラリに含まれている方の sortという関数が用いられる。arulesに含まれるsort()関数は、 by="" として指定した項目によって並べ替えを行う。例えば、信頼度(confidence)によって並び替えるのであれば、by="confidence" と指示する。

> grules3 <- sort(grules2,by="confidence")
> inspect( head(grules3) )

    lhs                                  rhs                support   
[1] {citrus fruit, root vegetables}   => {other vegetables} 0.01037112
[2] {tropical fruit, root vegetables} => {other vegetables} 0.01230300
[3] {curd, yogurt}                    => {whole milk}       0.01006609
[4] {other vegetables, butter}        => {whole milk}       0.01148958
[5] {tropical fruit, root vegetables} => {whole milk}       0.01199797
[6] {root vegetables, yogurt}         => {whole milk}       0.01453991
    confidence coverage   lift     count
[1] 0.5862069  0.01769192 3.029608 102  
[2] 0.5845411  0.02104728 3.020999 121  
[3] 0.5823529  0.01728521 2.279125  99  
[4] 0.5736041  0.02003050 2.244885 113  
[5] 0.5700483  0.02104728 2.230969 118  
[6] 0.5629921  0.02582613 2.203354 143

これを見ると、circuit fruitとroot vegetables の両方を買った人は同時に other vegetables を買っている割合が高いということが分かる。リフト値が 3.0296 なので、通常よりも高い確率で other vegetables を買うということがいえる。アソシエーション分析の手順について説明した。ルールを見つけるためには、適切なパラメータの値を指定しなければいけない。元のデータについて情報を得る方法について考えよう。アイテムの購入頻度を見るには itemFrequency()を用いる。個々のアイテムの割合 \(p(A)\) が表示される。

> itemFrequency(g0,type="absolute") %>% head()

      frankfurter           sausage        liver loaf               ham 
              580               924                50               256 
             meat finished products 
              254                64

並べ替えるには sort を用いる。値の大きいアイテムから順に並べたい場合には、 decreasing=TRUE (またはd=T) とする。または、小さい順に並べた上で、head() ではなく tail() として最後の数行を見ればよい。

> itemFrequency(g0) %>% sort(decreasing=T) %>% head()

      whole milk other vegetables       rolls/buns             soda 
       0.2555160        0.1934926        0.1839349        0.1743772 
          yogurt    bottled water 
       0.1395018        0.1105236

また、ルールを抽出する場合、前提部(lhs) や結論部(rhs) に来るアイテムを指定したいという場合もあるだろう。特定のアイテムを含んだルールだけを抽出したい場合には、 appearance=list()で指定する。

> grules5 <- apriori(g0,parameter=list(
+   support=0.005, confidence=0.7),
+   appearance =list( 
+     rhs="whole milk",
+     default="rhs"  ) )

Apriori

Parameter specification:
 confidence minval smax arem  aval originalSupport maxtime support minlen
        0.7    0.1    1 none FALSE            TRUE       5   0.005      1
 maxlen target  ext
     10  rules TRUE

Algorithmic control:
 filter tree heap memopt load sort verbose
    0.1 TRUE TRUE  FALSE TRUE    2    TRUE

Absolute minimum support count: 49 

set item appearances ...[1 item(s)] done [0.00s].
set transactions ...[169 item(s), 9835 transaction(s)] done [0.00s].
sorting and recoding items ... [120 item(s)] done [0.00s].
creating transaction tree ... done [0.00s].
checking subsets of size 1 done [0.00s].
writing ... [0 rule(s)] done [0.00s].
creating S4 object  ... done [0.00s].

例えば、ルールの結論部(rhs)に"whole milk"を含んだルールだけを抽出したいというときには、 appearance=list(rhs="whole milk",default="lhs") と指定する。このdefault="lhs" は"whole milk"以外の品目が前提部や結論部のどちらか一方のみに含まれているルールのみを求めたいという場合に、品目が出現する場所を指定する。この場合には、それ以外の商品が左辺ということなので、右辺は "whole milk"のみということになる。最後に、パラメータについてまとめておこう。 aprioriはトランザクション形式のデータを入力とし、信頼度や支持度の値を設定するときには、 parameter=list()の中で指定した。この他に、買い物のアイテムが増えてしまってルールがよく分からないという場合には、 maxlen=3という形で指定する。 maxlenとは前提部(lhs)と結論部(rhs)に出てくる両方のアイテムを合計したものである。また、特定の商品を含むものを考えるという場合には、 appearance=list()の中で指定する。ルールが抽出できた場合には、 inspect()でルールを表示する。ルールが多かった場合には、 head()やtail()で最初の行か最後の行を見る。その際、行を並び替えるためにsort() という関数を利用する。

6.4 まとめ

今回は、アソシエーション分析について説明した。条件つき確率を計算することで、因果関係を抽出した。このときの指標として、リフト値や信頼度などの 4つの指標を説明した。実際に計算する場合には、あらかじめ気になるルールについてのみ調べるのではなく、多くのアイテムの組み合わせについて調べて、その中から意味のあるルールを抽出することになる。リフト値は野球で言うと通常の打率と得点圏の打率を比較するようなものである。チャンスに強い選手を探し出すというものである。でも、通常よりも得点圏打率が高い選手であってもそもそもの得点圏打率が高くないのであればあまり意味がない。アプリオリはそこをうまく工夫し、頻出のアイテム集合についてのルールを調べつくすことができるようにしている。今回のこの計算のように何らかの判断基準を設定して計算すれば、ある結果を得ることができるが、しかし、出てきた結果が有用であるかどうか、を判断するのは人であって、結果が出たからといって何でも意味があるわけではない。

参考文献

[1]. R. Agrawal,T.Imielinski and A.Swami, “Database mining: a performance perspective”, IEEE Transactions on Knowledge and Data Engineering, 5(6),pp914-925,1993

[2]. Michael Hahsler, Kurt Hornik, and Thomas Reutterer, “Implications of probabilistic data modeling for mining association rules”, pp598–605, In M. Spiliopoulou, R. Kruse, A. N{"u}rnberger, C. Borgelt,and W. Gaul, “From data and information analysis to knowledge engineering” , Springer-Verlag,2006,

[3]. 金明哲,“R によるデータサイエンス(第2版)”,森北出版,2017

演習

1.　Groceries は実際のある地域のショッピングセンターでの 1ヶ月の買い物データであったが、この他にもある期間にダウンロードされた文献リストであるEpubや職業や年齢などの15の変数からなる約5万人への調査結果である Adultや収入について14個の変数からなる Incomeがある。Income は @hastie でも取り上げられている例題データである。この本は英語であればWebサイトからPDFをダウンロードできる。

> data(Epub)
> as(Epub,"data.frame") %>% head()

                         items transactionID           TimeStamp
10792                {doc_154}  session_4795 2003-01-02 10:59:00
10793                {doc_3d6}  session_4797 2003-01-02 21:46:01
10794                {doc_16f}  session_479a 2003-01-03 00:50:38
10795 {doc_11d,doc_1a7,doc_f4}  session_47b7 2003-01-03 08:55:50
10796                 {doc_83}  session_47bb 2003-01-03 11:27:44
10797                {doc_11d}  session_47c2 2003-01-04 00:18:04