12 主成分分析
データによっては、非常に多くの項目からなる多次元のデータを扱うことがある。多次元のデータから持っている情報量をそのままに次元を減らす方法として主成分分析がある。ここでは主成分分析の考え方について説明し、Rでの方法を説明する。
キーワード
主成分分析、次元圧縮、分散共分散行列、 相関行列
12.1 主成分分析の概要
まずは、主成分分析のイメージを図で考えてみよう。データが図 1.1 のように散らばっているものとする。 本来、図のような点を取り囲む曲線はないが、理解しやすいように曲線があるものとして考えてみよう。データは平面上に近い形で散らばっていて、この平面に垂直な向きへのばらつきは小さいものとする。
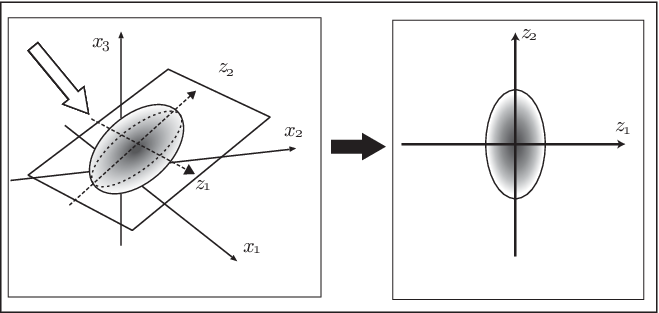
このとき、このグラフを様々な角度から眺めることができるとして、一体どの角度から見たら、このデータの特徴を表していると思うのか、 考えてみよう。 すると、多くの人は図の矢印(図1.1の左側の図中)で示した ように平面の垂直な方向からと 考えるのではないだろうか。 このように、もしどこかの方角から見た成分を無視しなければならないとしたら、 値のさほど変わらない、ばらつきの少ない方向を無視することにするだろう。 このように、主成分分析は、線形な座標変換を行い、それによって得られた成分のうち、 情報量の多いものから順に考えることで、情報量の損失をなるべく抑えつつ次 元を減らそうとする方法である。
では、このイメージを踏まえて、定式化することを考えてみよう。\(r\)次元のデータがあり、それを \((x_1,x_2,\cdots, x_r)\) とする。 例えば、今、体格について検討することを考え、\(x_1\)は身長、\(x_2\)を体重、\(x_3\)が足の大きさ、といったものを表していると考えよう。 ただし、身長のデータを\(x_1\)と書いたが、実際には多くの人のデータを集めることになる。 そこで、サンプルや事例を表すときには、添字の\((p)\)で表すことにする。 つまり、\(n\)人のデータを表す場合には、一人目の身長を \(x_1^{(1)}\)、\(n\) 人目の身長を \(x_1^{(n)}\) というように表すことにしよう。 そして、その平均値をそれぞれ \((\mu_1,\mu_2,\cdots,\mu_r)\)、分散を \((\sigma_1^2,\sigma_2^2,\cdots,\sigma_r^2)\) とする。また、共分散を\(\sigma_{ij}\) と表す。 \(\sigma_{11}=\sigma_1^2\) である。 ここで扱うデータとは様々な種類の属性を持つものがあるだろう。例えば、\(r\)個の科目の成績を意味しているかもしれないし、 身長や体重といったものを表しているかもしれない。このとき、身長をセンチメートルで表すか、メートルやインチで表すのかといったように、 単位によって違うのでは都合が悪い。そこで、それぞれのデータの平均が\(0\)になるようにする。 これを中心化という。 \[ {x_i^{(p)}}^{\prime} = (x_i^{(p)}-{{\mu_i}}) \tag{12.1}\] さらに、標準偏差で割ることで分散を1にすることを標準化という。 \[ {x_i^{(p)}}^{\prime\prime} = \frac{ x_i^{(p)}-{{\mu_i}} }{\sigma_i } \tag{12.2}\] となる。 今後、このようにして、変換されたデータを \(y_1,y_2,\cdots,y_r\) とする。 さて、先ほどの 変換について考えてみよう。 変換によって得られる\(m\) 個の成分を\((z_1,z_2,\cdots,z_m)\)とする。\(z_i\) は
\[\begin{eqnarray} z_1 &=& a_{11} y_1 + a_{12}y_2+\cdots+ a_{1r} y_r \\ z_2 &=& a_{21} y_1+ a_{22}y_2 +\cdots+ a_{2r} y_r \\ &\vdots & \\ z_m &=& a_{m1} y_1 + a_{m2}y_2+\cdots+ a_{mr}y_r \end{eqnarray}\]と書ける。 この新しい成分のことを主成分といい、 \(z_i\) を第\(i\)主成分という。変換した個々のデータの値のことを 主成分得点という。 新しい成分の次元がもともとの成分の次元より増えることはないので、 \(m\leq r\) である。 行列で表すと、 \[\left( \begin{array}{c} z_1 \\ z_2 \\ \vdots \\ z_m \end{array} \right) = \left( \begin{array}{cccc} a_{11}&\cdots&\cdots&a_{1r} \\ \vdots&\ddots&\ddots&\vdots \\ a_{m1}&\cdots&\cdots&a_{mr} \\ \end{array} \right ) \left( \begin{array}{c} y_1\\ y_2\\ \vdots \\ y_r \end{array} \right) \] となる。ここで、\(a_{i1}\)、\(a_{i2}\)、\(\cdots\)、\(a_{ir}\) という量は新たな軸の方向に対応する量で、値は1つには定まらない。 \[ \sum_{j=1}^{r}a_{ij}^2 =1 \] という条件を加えることにする。
12.2 主成分の導出
2次元の場合について考えてみよう。まず、データが図のように分布しているようなものを考えてみる。標準化によってどの軸の分散も \(1\) になるようにしているものとする。 (Figure 12.2)に示すように点\(\boldsymbol{y}^{(i)}\) があるとき、新たな軸\(z\)に移す時、その原点との距離が その軸で表すことができる分散になり、 逆にそれに直交する部分の情報が失われるということになる。
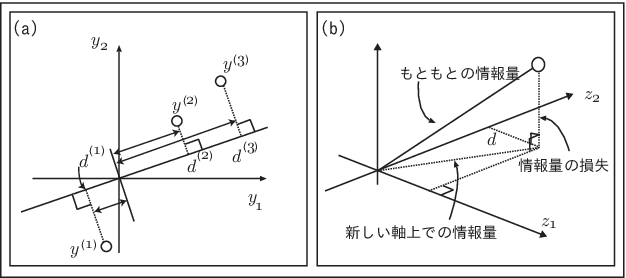
2次元の場合に \(z_1\)や\(z_2\)といった軸を求めることを考える。 (Figure 12.3) に示すような軸を考え、 \(a_{1}^2+a_2^2 =1\) が成り立っているものとする。 今、一辺の長さが、\(a_1\)、\(a_2\)の直角三角形 を考えると、 \(z_1\)軸上の点 \(z_1=a_1y_1^{(1)}+a_2y_2^{(1)}\) は点(\(y_1^{(1)}\),\(y_2^{(1)}\))から \(z_1\)軸へ下ろした垂線の足に なっている。
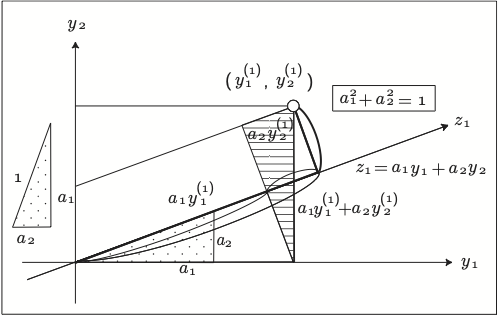
そして、原点との距離が \[ (d^{(1)})^2 = (a_1y_1^{(1)}+ a_2y_2^{(1)})^2 \] となるので、全てのサンプルについて足し合わせると
\[\begin{eqnarray} \sum_{p=1}^{N}(d^{(p)})^2 &=& \sum_{p=1}^{N}\{(a_1y_1^{(p)})^2+ (a_2y_2^{(p)})^2+2a_1a_2y_1^{(p)}y_2^{(p)} \} \\ &=& a_{1}^2\sum_{p=1}^{N}(y_1^{(p)})^2 +a_{2}^2\sum_{p=1}^{N}(y_2^{(p)})^2 +2a_{1}a_{2}\sum_{p=1}^{N}(y_1^{(p)}y_2^{(p)}) \\ &=& S_{11} a_{1}^2+2S_{12}a_{1}a_{2}+S_{22}a_{2}^2 \end{eqnarray}\]となる。これを\(n-1\)で割ると \[ U(a_1,a_2) = \sigma_{1}^2 a_{1}^2+2\sigma_12 a_{1}a_{2}+\sigma_{2}^2a_{2}^2 \] となる。もし、データを標準化している場合には、 \(\sigma_{1}=\sigma_{12}=1\)、\(\sigma_{12}=\rho_{12}\) なので、 \[ U(a_1,a_2) = a_{1}^2+2\rho_{12}a_{1}a_{2}+a_{2}^2 \] となる。 このように、データの分散共分散行列(または相関行列)を用いて表現することができる。 あとは、これを制約条件 \[ a_{1}^2+a_2^2 =1 \] のもとで最大となるような \(a_{1}\)、\(a_{2}\) を求める。 制約条件のある最大最小問題には ラグランジュの未定乗数法を用いることができる [^pca-3]。 最大最小を与える変数の値を 求める場合には、 \[G(a_1,a_2,\lambda)=U(a_1,a_2)-\lambda (a_1^2+a_2^2-1) \] を\(a_1\)、\(a_2\)、\(\lambda\)で偏微分して、最終的に
\[\begin{eqnarray} a_1+r_{12}a_{2}-\lambda a_1 &=& 0\\ r_{12} a_1+a_{2}-\lambda a_2 &=& 0 \\ a_1^2+a_{2}^2 &=& 1 \end{eqnarray}\]を満たすような\(a_1\)、\(a_2\)を求めればよいということになる。 行列で書くと \[ \left( \begin{array}{cc} 1 & r_{12} \\ r_{12} & 1 \end{array} \right) \left( \begin{array}{c} a_1 \\ a_2 \end{array} \right) = \lambda \left( \begin{array}{c} a_1 \\ a_2 \end{array} \right) \tag{12.3}\] であり固有値、固有ベクトルを求める計算ということになる。 今回は第1主成分として計算したが、第2主成分であっても 同様に計算することになり、 結局、(Equation 12.3) と 同じ固有ベクトルを求めることになる。 また、この行列は対称行列で。第1主成分と第2主成分が 独立と成るように選ぶことができる。 2行2列の固有値は多くて2個である。どちらの固有ベクトルを用いればよいのだろうか。 式(Equation 12.3) を満たす固有値を \(\lambda^{*}\) 、固有ベクトルを \[ \boldsymbol{a^*} = \left( \begin{array}{c} a_{1}^{*} \\ a_{2}^{*} \end{array} \right) \] として、主成分の分散を求めてみると、分散は \(U(a_1,a_2)\) だから、
\[\begin{eqnarray} U(a_{1}^{*},a_{2}^{*}) &=& {a_1^{*}}^2+2r_{12}a_{1}^{*}a_2^{*}+{a_2^{*}}^{2} \\ &=& a_1^{*}(a_1^{*}+r_{12}a_{2}^{*})+a_2^{*} (r_{12}a_{1}^{*}+a_2^{*}) \\ &=& a_1^{*}(\lambda^{*} a_1^{*})+a_2^{*}(\lambda^{*} a_2^{*}) \\ &=& \lambda^{*} ({a_1^{*}}^2+{a_2^{*}}^2) = \lambda^{*} \end{eqnarray}\]となる。つまり、求めた主成分のばらつき具合である分散は、求める行列の固有値に等しい。 したがって、固有値のうち大きい値に対応する固有ベクトルを 求めればよいということになる。 一般に \(r\) 次元のデータの場合も同様に計算することができ、分散が最大になるという条件を求めると、 \[ A= \left( \begin{array}{cccc} \sigma_{1}^2&\sigma_{12}&\cdots&\sigma_{1r} \\ \sigma_{21}&\sigma_{2}^2&\cdots&\sigma_{2r} \\ \vdots&\vdots&\ddots &\vdots \\ \sigma_{r1}&\sigma_{r2}&\cdots&\sigma_{r}^2 \\ \end{array} \right ) \tag{12.4}\] または、標準化した後であれば、 \[ B= \left( \begin{array}{cccc} 1 &\rho_{12}&\cdots&\rho_{1r} \\ \rho_{21}&1&\cdots&\rho_{2r} \\ \vdots&\vdots&\ddots &\vdots \\ \rho_{r1}&\rho_{r2}&\cdots&1_{rr} \\ \end{array} \right ) \tag{12.5}\] #| message: FALSE に対して、 係数を \[ A \boldsymbol{a_i} = \lambda_{i} \boldsymbol{a_i} \] ただし \[ \boldsymbol{a_i}= \left( \begin{array}{c} a_{i1} \\ a_{i2} \\ \vdots \\ a_{ir} \end{array} \right) \] と書くことができる。すなわち、 \(r \times r\)の行列の固有値 \(\lambda_i\) \((i=1,2,\cdots,r)\)を求めることになる。 ここで、共分散については、\(\sigma_{ij}=\sigma_{ji}\) が成り立つので、これは行列としては対称行列である。対称行列の固有ベクトルは 互いに直交することが知られている。 また、分散共分散行列(相関行列)は半正定値、すなわち 固有値がすべて0以上になることが知られている。 (Equation 12.4) または式(Equation 12.5) で表される行列の固有値を求め、 そのうち最も大きいものから順に、第1主成分、第2主成分 というように 定めていけばよい。 また、第 \(i\) 成分の分散はその固有値の値に等しくなる。したがって、どの成分までを考えるかは固有値の大きさで判断すればよい。 そこで、この固有値を \(\lambda_1\geq\lambda_2\geq\cdots\geq\lambda_r\geq 0\)として、 \[ \frac{\lambda_i}{\lambda_1+\lambda_2+\cdots+\lambda_r} =\frac{\lambda_i}{\displaystyle\sum_{k=1}^r \lambda_k} \] の値を第\(i\)主成分の寄与率という。また、第1主成分から第\(i\)主成分までの寄与率の合計 \[ \frac{\lambda_1+\cdots+\lambda_i}{\lambda_1+\lambda_2+\cdots+\lambda_r} =\frac{\displaystyle\sum_{j=1}^i \lambda_j}{\displaystyle\sum_{k=1}^r \lambda_k} \] を第1主成分から第\(i\)主成分までの累積寄与率という。 累積寄与率の目安として \(0.8\) が用いられる。
12.3 2次元の場合の例
このことを例をもとに考えてみよう。以下の表は、Rに含まれるデータで30歳から39歳までのアメリカ人女性15人の身長と体重を 集めたもの(women)を標準化したものである。
> women %>% head() height weight
1 58 115
2 59 117
3 60 120
4 61 123
5 62 126
6 63 129これを2次元にプロットすると、(Figure 12.4)のようになる。
> women %>%
+ mutate(height=scale(height),weight=scale(weight)) %>%
+ ggplot()+geom_point(aes(x=height,y=weight))+theme_bw()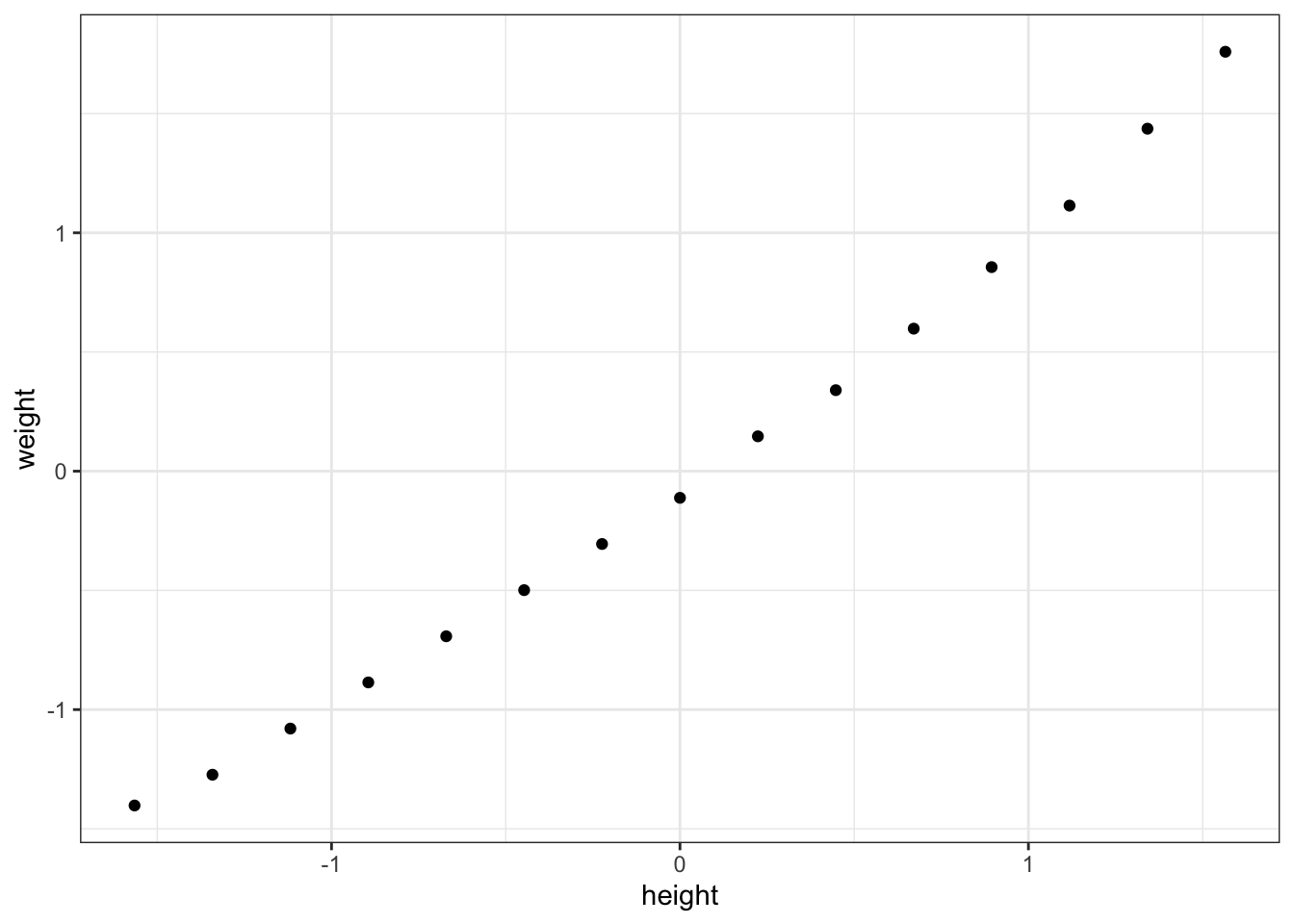
これを見ると身長と体重のデータはほぼ一直線上にあることがわかる。このときの共分散(実際には、標準化しているので相関係数)の値は、 0.995 である。すると、 \[
\left(
\begin{array}{cc}
1 & 0.996 \\
0.996 & 1
\end{array}
\right)
\left(
\begin{array}{c}
a_1 \\
a_2
\end{array}
\right)
=
\lambda
\left(
\begin{array}{c}
a_1 \\
a_2
\end{array}
\right)
\]、
となるような \(\lambda\)、\(a_1\)、\(a_2\)を求めることになる。 2次元の行列式は2次方程式を解けばよく、実際に計算すると、固有値は、\(1.996\)、\(0.004\)となり、 それを満たすような固有ベクトルを求めると \[
\left(
\begin{array}{c}
0.707 \\
0.707
\end{array}
\right)
\]、 \[\left(
\begin{array}{c}
-0.707 \\
0.707
\end{array}
\right)\] となる。ちなみに、この場合、第1主成分の寄与率が \[
\frac{1.996}{1.996+0.004}=0.998
\] となるので、この例では第1主成分だけで十分である。 では、これをRで計算してみよう。prcomp()という関数を用いる。 手順は、データをw1で読み込む。1行目が名前なので、その列を除いた prcomp(w1[,-1]) として主成分分析を行う。 その結果を今、w2という名前であるとすると、手順は
> pr_w <- prcomp(women,scale=TRUE)
> pr_wStandard deviations (1, .., p=2):
[1] 1.41261982 0.06712103
Rotation (n x k) = (2 x 2):
PC1 PC2
height 0.7071068 0.7071068
weight 0.7071068 -0.7071068prcompは自動的に中心化をして計算するが、指定しない場合に標準化はしない。もし、標準化したい場合はscale=TRUEとする。中心化もしない場合には、center=Fと指定する。 計算結果を見ると、標準偏差と固有ベクトルの値が表示される。この標準偏差は\(U(a_1,a_2)\)の平方根の値であり、固有値の平方根と一致する。この値を二乗したものが固有値の値である。 summary()という関数で結果の要約を見ることができる。
> summary(pr_w)Importance of components:
PC1 PC2
Standard deviation 1.4126 0.06712
Proportion of Variance 0.9978 0.00225
Cumulative Proportion 0.9978 1.00000となる。最初のStandart deviationは主成分の標準偏差である。 2行目が寄与率、3行目が累積寄与率を表している それぞれの主成分得点はpr_w$xで見ることができる。 これを図にしてみよう。ggplotではよく使われるデータを 簡単に可視化するための関数として ggfortifyというパッケージがある。
> require(ggfortify)
> autoplot(pr_w,loadings=TRUE, loadings.label=TRUE)+
+ theme_bw()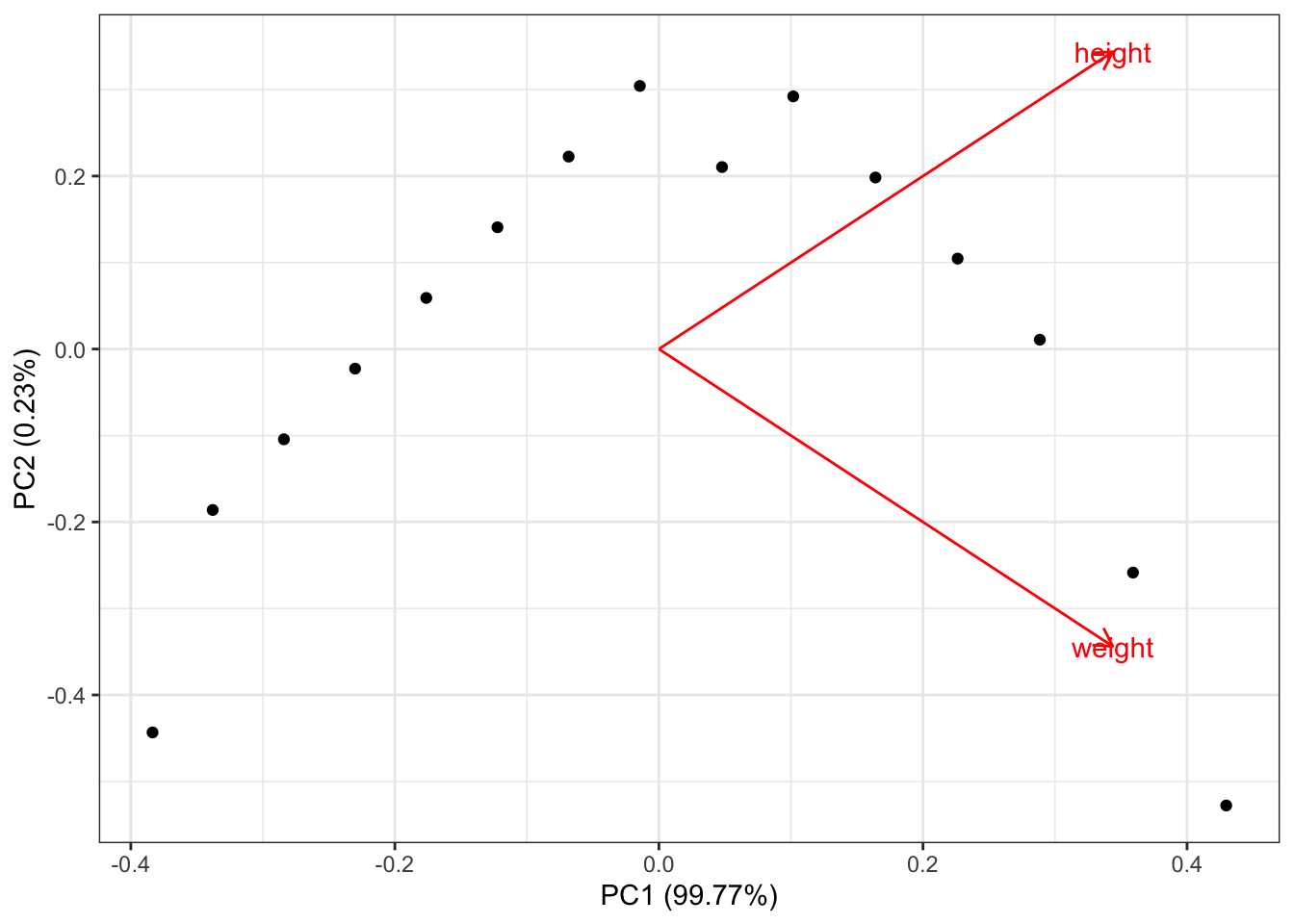
ggfortify の関数であるまずautoplot()という関数を用いる。これを見るとheightが身長が1、体重が0, weightが身長が0、体重が1 の人の場所。 つまり右に行くほど、身長や体重の値が大きい人がいることがわかる。 主成分の寄与率が座標に表記され、実際の点自体は縦軸と横軸が 同じ範囲になるように拡大縮小されている。 実際に計算される主成分をそのまま散布図にすると次のようになる。
> ggplot(data=pr_w$x)+geom_point(aes(x=PC1,y=PC2))+theme_bw()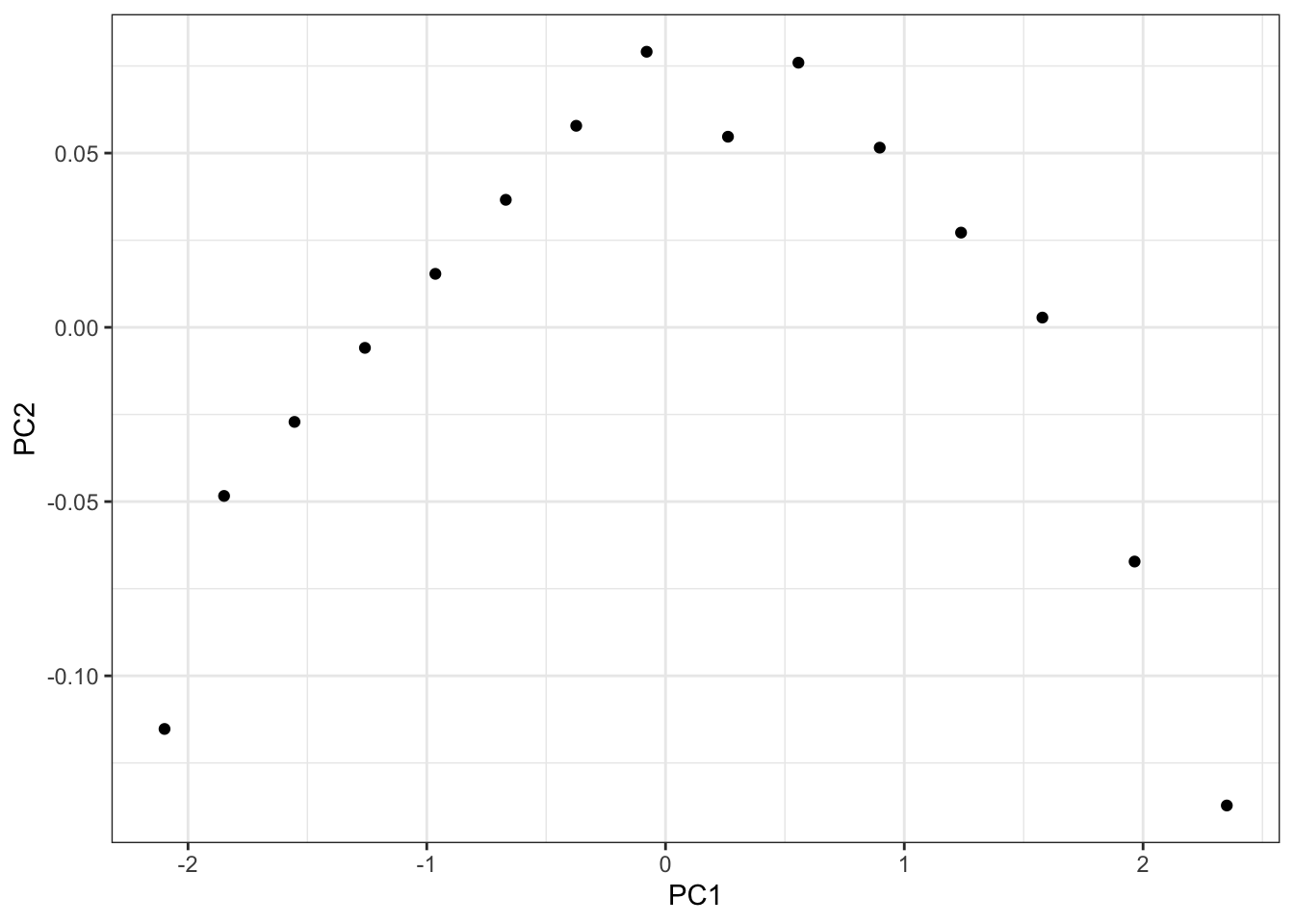
もう一つの例として、irisを扱う。irisは4種類の観測値と 種を表す5列からなるデータである。この4列の部分を減らす (次元圧縮ともいう)ことを考える。 出てきた
> pr_iris <- prcomp(iris[,1:4],scale=TRUE)
> summary(pr_iris)Importance of components:
PC1 PC2 PC3 PC4
Standard deviation 1.7084 0.9560 0.38309 0.14393
Proportion of Variance 0.7296 0.2285 0.03669 0.00518
Cumulative Proportion 0.7296 0.9581 0.99482 1.00000これを見ると2次元まで寄与率が 95%となっている。 主成分 $x$は行列形式なので、データフレーム形式にして、最後に 元の種を付け加える。
> pr_out <- pr_iris$x %>% data.frame() %>%
+ mutate(Species=iris$Species)
> head(pr_out) PC1 PC2 PC3 PC4 Species
1 -2.257141 -0.4784238 0.12727962 0.024087508 setosa
2 -2.074013 0.6718827 0.23382552 0.102662845 setosa
3 -2.356335 0.3407664 -0.04405390 0.028282305 setosa
4 -2.291707 0.5953999 -0.09098530 -0.065735340 setosa
5 -2.381863 -0.6446757 -0.01568565 -0.035802870 setosa
6 -2.068701 -1.4842053 -0.02687825 0.006586116 setosaこれを種子ごとに色分けすると
> ggplot(pr_out)+geom_point(aes(x=PC1,y=PC2,color=Species))+theme_bw()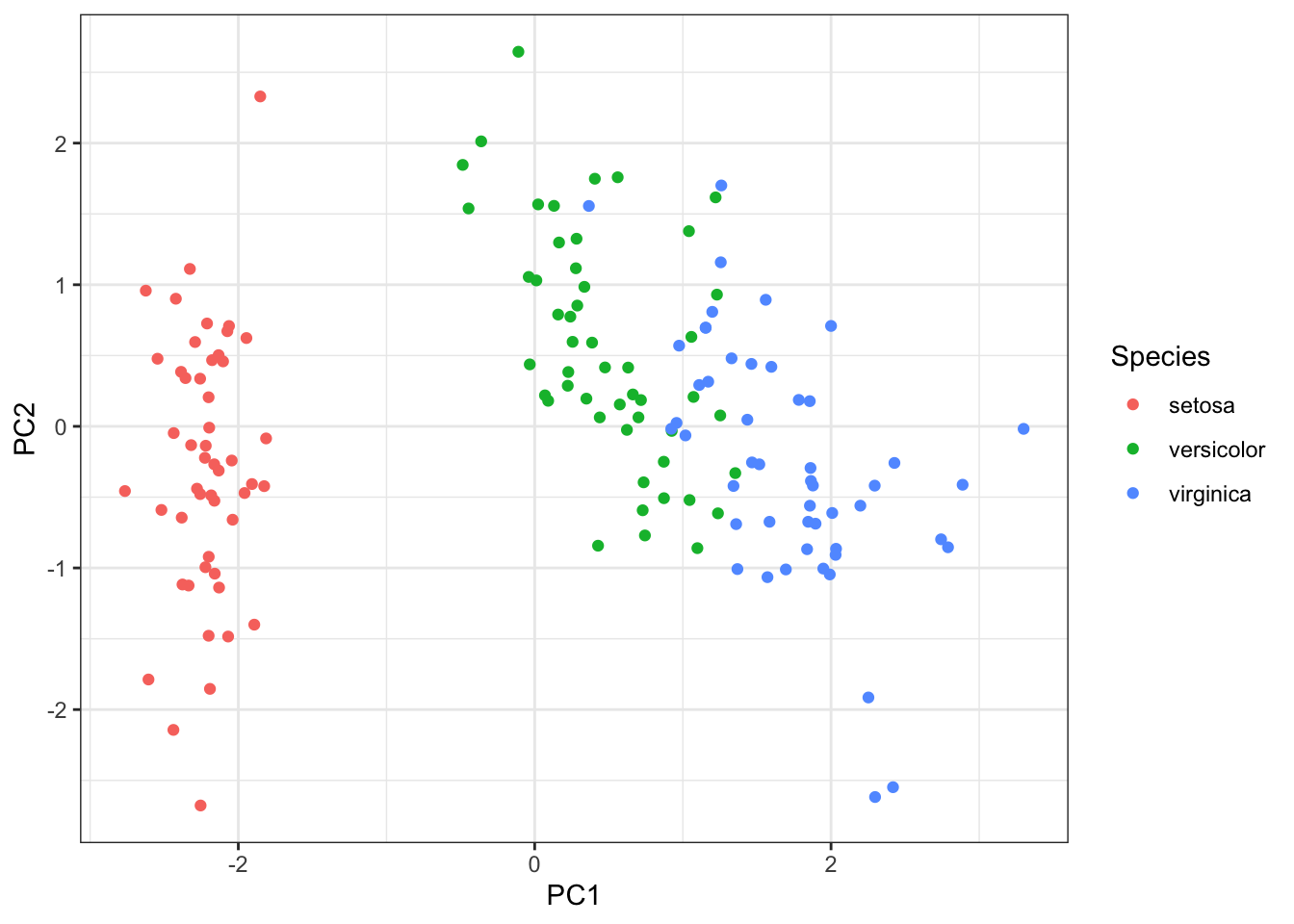
となる。このように4次元のものを圧縮して表示することができる。
12.4 まとめと展望
主成分分析とは、多くの変数をより少ない変数で記述することを目的としたものであった。 主成分分析でも回帰分析でもどちらもその変数の平均値を通る。また出てきた行列もほぼ同じである。 そこで、ここでは、その違いについて述べておこう。 回帰分析では、目的変数を1次式によって表し、目的変数との誤差を計算した。 一方、主成分分析ではそのデータを代表するような新しい軸を設定し、 その軸上に射影された点を点の代表の点とするものであり、 目的変数を持たない。 そして、回帰直線では目的変数を表すため、その誤差は軸に沿って測る。一方、主成分分析は軸との距離が最小になるように求めているので、距離の測り方は軸に垂直になるように測る。 この違いを図示すると(Figure 12.5)のように表せる。
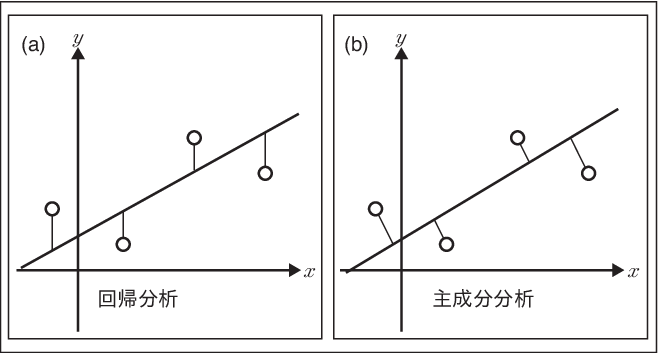
参考文献
[1]. 林賢一,下平英寿,Rで学ぶ統計的データ解析,講談社,2020
[2]. 中村,永友,Rによるデータサイエンス2『多次元データ解析法』, 共立出版,2009
[3]. 金明哲,“R によるデータサイエンス(第2版)”,森北出版,2017
演習
次の計算は標準正規乱数を Chapter 2 で計算した行列で変換したものである。値を色々変えて 主成分分析を行ったり、分散共分散行列することができる。
> N <- 1000
> mat <- c(1,2,3,-4)
> x <- rnorm(N)
> y <- rnorm(N)
> p_before <- cbind(x,y)
> A <- matrix(mat,ncol=2,nrow=2)
> eigen(A)
> p_after <- p_before %*% t(A)
> prcomp(p_after)mat <- c(1,2,3,-4) の値を色々と変えてシミュレーションしてみよ 。その際、eigen(A) とprcomp の固有値を比較してみよ。