5 確率分布

データを分析する際によく利用される確率分布について概説する。 R では様々な確率分布について、その分布に従う乱数を発生させる関数が提供されている。そこで、こうした乱数を用いて確率分布同士の関係を見るシミュレーションについて説明する。最後にファクター（因子）と呼ばれるデータ型について説明する。

キーワード

確率分布、標本分布、乱数、ファクター

5.1 確率分布

「明日の天気が晴れであるかどうか」や「コインを投げて表が出る」のように２種類のどちらかであるような試行を ベルヌイ試行といい、「天気が晴れる」、「コインの表が出る」といった試行によって起こる結果のことを事象という。ベルヌイ試行を繰り返し行い、表が出る回数 \(X\) について調べることを考えよう。この変数 \(X\) は起こる回数によって異なる確率となる。このようにある変数が確率と対応づけられるとき、その変数を 確率変数 という。確率変数は、この成功回数のような離散値となることもあれば、待ち時間のように連続値となる事もある。そして、確率変数と確率との対応を 確率分布 という。ある確率変数が \(n\) 通りの値 \(x_i\) を取るものとし、それぞれの確率を\(p_i\) として

\[\begin{eqnarray} P(X=x_i) &=& p_i \end{eqnarray}\]

というように書く。2種類の事象のうち、ある一方の事象が起こる確率を \(p\)（\(0 \leqq p \leqq 1\)）とする。 \(n\) 回のベルヌイ試行でこの事象が起こる回数が \(k\) 回となる確率は

\[\begin{eqnarray} P(X=k) &=& {}_{n}C_{k} p^{k}(1-p)^{n-k} \label{eqn:binom} \end{eqnarray}\]

と表すことができる。この確率変数\(X\) が従う確率分布を二項分布という。この確率分布は、\(n\) と \(p\)の値によって決まる。このように確率分布を特徴付ける量を母数（パラメータ）という。ある確率分布が与えられた時に、その分布に従う確率変数から出る値として予測される値を期待値という。期待値と分散は

\[\begin{eqnarray} E[X] &=& \sum_{i=1}^{\infty} x_iP(x_i) \\ V[X] &=& E[(X -\bar{X})^2] = \sum_{i=1}^{\infty} (x_i-m)^2 P(x_i) \end{eqnarray}\]

と計算することができる。二項分布の場合、

\[\begin{eqnarray} E[X] &=& np \\ V[X] &=& npq \end{eqnarray}\]

となる。ある事象が確率 \(p\)で起こるベルヌイ試行を繰り返し行うとき、この事象が初めて起こるまでの試行回数を \(X\) とすると、\(X=k\) となる確率は

\[\begin{eqnarray} P(X=k) &=& (1-p)^{k-1}p \end{eqnarray}\]

と書くことができ、\(X\) が従う確率分布を幾何分布 という。期待値と分散は

\[\begin{eqnarray} E[X] &=& \frac{1}{p} \\ V[X] &=& \frac{1-p}{p} \end{eqnarray}\]

と求まる。次に、確率変数 \(X\)が連続値を取る場合を考える。例として、身長を測定することを考えよう。身長が \(160\) cm ということがある。しかし、実際には無限に精度を高めて測定することができるとすると、ちょうど \(160.0\)cmであることはあまりない。つまりその確率はとても小さくなると考えられる。そのような場合は、\(X\) が \(160\)cm になる確率を考えるのではなく \(159.9\)cmから\(160.1\)cmというように、ある範囲にある確率を考える方が有効だろう。このように確率変数が連続の値を取る場合には、 \(a \leqq X \leqq b\) である確率を

\[\begin{eqnarray} P(a\leqq X \leqq b) &=& \int_{a}^{b} f(x) dx \end{eqnarray}\]

という形で考えた方が良い。そこで、この \(f(x)\)のことを確率密度関数と呼ぶ。また、

\[\begin{equation} F(x) = P(X \leqq x) = \int_{-\infty}^{x} f(t) dt \end{equation}\]

で表される関数を（累積）分布関数という。例として、平均\(\mu\)、分散\(\sigma\)である正規分布（これを\(N(\mu,\sigma^2)\)と書く。）の確率密度関数は次のように表される。

\[\begin{eqnarray} f(x) &=& \frac{1}{\sqrt{2\pi\sigma^2} }\exp(-\frac{(x-\mu)^2}{2\sigma^{2}}) \end{eqnarray}\]

と表される。\(N(0,1)\) のことを特に 標準正規分布 という。たとえば、確率変数\(X\)が標準正規分布にしたがう時、

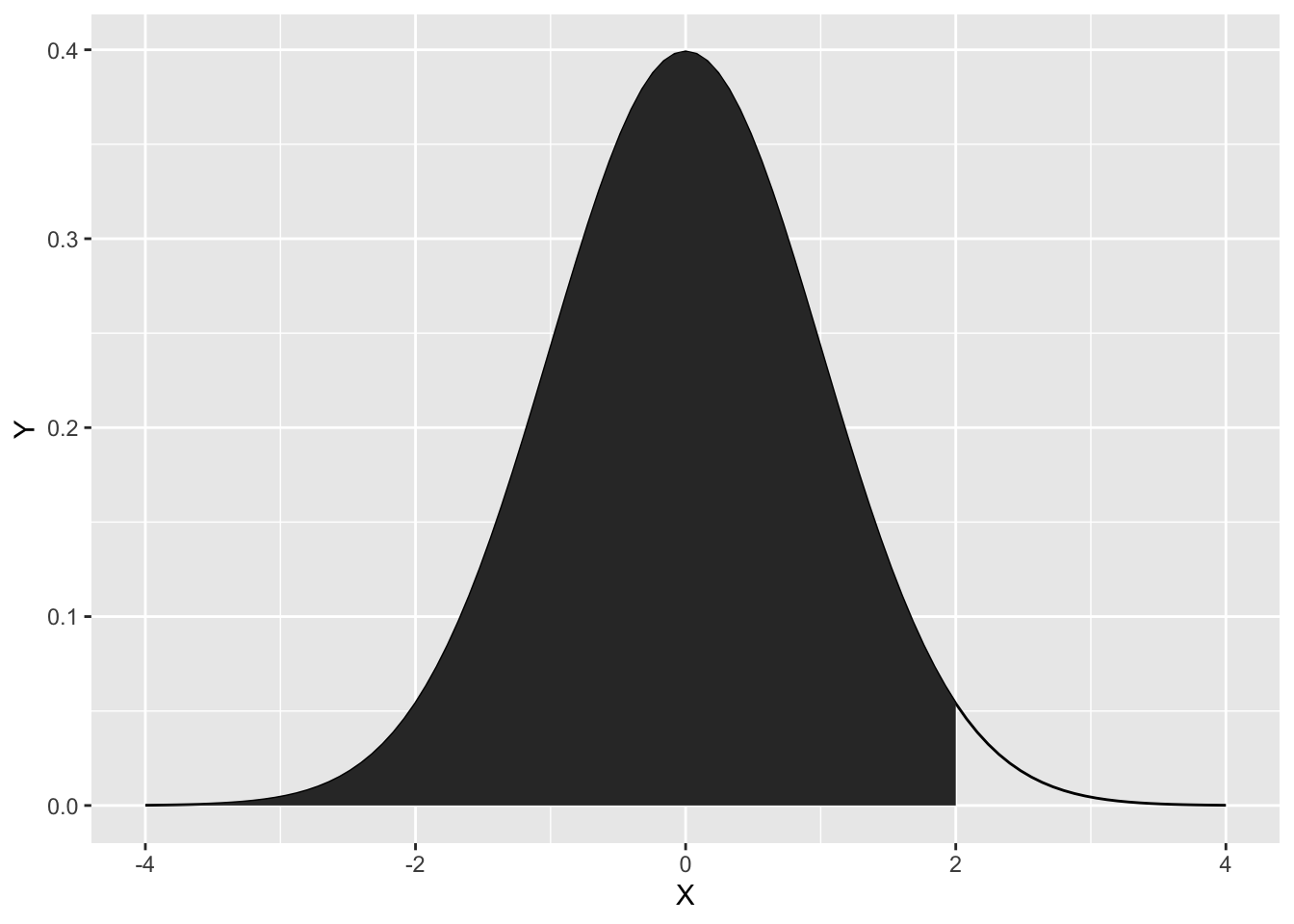
Figure 5.1 に示すような \(X\leqq 2\)となる確率\(P(X \leqq 2)\)は \[ P(X \leqq 2) = \int_{-\infty}^{2}\frac{1}{\sqrt{2\pi}} \exp(-\frac{t^2}{2}) dt \] を計算することになる。このような計算を今後 R を用いて行う。連続分布の場合の期待値と分散も離散分布同様に定義でき、

\[\begin{eqnarray} m &=& E(X) =\int_{\infty}^{\infty} x f(x) dx \\ V(X) &=& \int_{\infty}^{\infty} (x-m)^2 f(x) dx \end{eqnarray}\]

を計算することで求めることができる。実際に計算すると

\[\begin{eqnarray} \int_{\infty}^{\infty} t \cdot \frac{1}{\sqrt{2\pi\sigma^2} }\exp(-\frac{(t-\mu)^2}{2\sigma^{2}}) dt &=& \mu \\ \int_{\infty}^{\infty} (t-\mu)^2 \cdot \frac{1}{\sqrt{2\pi\sigma^2} }\exp(-\frac{(t-\mu)^2}{2\sigma^{2}}) dt &=& \sigma^2 \end{eqnarray}\]

が成り立つ。ある変数 \(x\) が有限区間 \(x \in [a,b]\) の範囲で等確率で起こるとき、確率密度関数は

\[\begin{equation} P(X\leq x) =\frac{1}{b-a} \end{equation}\]

と書くことができる。これを 一様分布 という。その期待値と分散は

\[\begin{eqnarray} E(X) &=& \frac{a+b}{2} \\ V(X) &=& \frac{(b-a)^2}{12} \end{eqnarray}\]

となる。

5.2 指数分布とポアソン分布

二項分布において、期待値である \(np=\lambda\) を一定にした条件で \(n\) を大きくした極限を考えると

\[\begin{equation} P(X=k) = \frac{e^{-\lambda}{\lambda^k}} {k!} \end{equation}\]

となる。この \(X\) が従う分布をポアソン分布という。 \(n\) を大きくすると \(p=\frac{\lambda}{n}\) は小さい値となる。とはいえ、全く起きないということはなく、平均的に \(\lambda\) 回起こる。このように、ポアソン分布は滅多に起きない事象が起こる回数を考えるときに使われる。このとき、期待値と分散は

\[\begin{eqnarray} E[X] &=& \lambda \\ V[X] &=& \lambda \end{eqnarray}\]

となる。また、幾何分布において、\(x=\frac{k}{n}\) として、\(np=\lambda\) として \(n\) を無限に大きくすると

\[\begin{eqnarray} P(X=x) &=& \lambda \exp(-\lambda x) \end{eqnarray}\]

となる。この\(X\)が従う分布を指数分布という。幾何分布が初めて起こるまでの回数であったが、指数分布は次に人に出会うまでの待ち時間などを表すときに使われる。ポアソン分布での生起する間隔の分布は指数分布となる。期待値と分散は

\[\begin{eqnarray} E[X] &=& \frac{1}{\lambda} \\ V[X] &=& \frac{1}{\lambda^2} \end{eqnarray}\]

となる。指数分布は次に生起するまでの待ち時間を表したが、次の \(k\) 回が起こるまでの時間は次の式で表される。

\[\begin{eqnarray} P(X=x) &=& \frac{\lambda^{k}}{\Gamma(k)} x^{k-1}e^{-\lambda x } \end{eqnarray}\]

これをガンマ分布という。ここで \(\Gamma(z)\) は階乗を拡張した関数で、実部が正の複素数\(z\) を用いて

\[\begin{eqnarray} \Gamma(z) &=& \int_{0}^{\infty} t^{z-1}\exp(-t) dt \end{eqnarray}\]

で定義される。\(k\) が自然数のとき、\(\Gamma(k) = (k-1)!\) である。期待値と分散は

\[\begin{eqnarray} E[X] &=& \frac{k}{\lambda} \\ V[X] &=& \frac{k}{\lambda^2} \end{eqnarray}\]

となる。

5.3 確率分布に関する関数

Rでは確率分布に関する関数としては4種類の関数がある。正規分布の場合には

Table 5.1: 正規分布に関する関数
関数名	説明
`dnorm(x,mean,sd)`	確率密度関数 \(f(x)\) の値
`pnorm(x,mean,sd)`	分布関数\(P(X<x)\) の値
`qnorm(p,mean,sd)`	確率点。`pnorm` が`p`となる`x`の値
`rnorm(N,mean,sd)`	正規乱数を`N`個

省略時既定値が \(\mu=0\)、\(\sigma=1\) となっているので、省略すると標準正規分布に関する関数となる。 Figure 5.1 に示すような色塗りの部分の面積は

> pnorm(2,0,1)

[1] 0.9772499

と求めることができる。正規分布以外にもさまざまな関数がある。主な確率に関する関数を表 Table 5.2 に示す。用途に応じて関数名の前にd、p、q、rをつけて用いる。接頭辞の意味は正規分布における意味と同じである。

Table 5.2: 代表的な確率分布の関数
関数名	分布名	パラメータ
`binom`	二項分布（離散）	size,p
`geom`	幾何分布（離散）	prob
`pois`	ポアソン分布（離散）	lambda
`unif`	一様分布（連続）	min,max
`exp`	指数分布（連続）	rate
`gamma`	ガンマ分布（連続）	shape,rate
`chisq`	カイ2乗分布（連続）	df
`t`	t分布（連続）	df
`f`	f分布（連続）	df1, df2

5.4 標本分布

同じ母集団から複数のデータ（\(N\) 個のデータ）を取り出すことを考えよう。個々のデータはどれも独立で同じ確率分布に従うとする。その確率変数 \(X_i\) について、 \(\mu=E[X_i]\)とし、\(\sigma^2={\rm Var}[X_i]\) （\(i=1,2,\cdots,N\)）、分散が有限であるとする。このとき、この \(N\)個の確率変数から計算される \(\sum_{i=1}^N X_i\) は \(N(N\mu,N\sigma^2)\) に従うことが知られている。これを中心極限定理 という。 \(N\) が大きければ \[ \bar{X}=\frac{1}{N}\sum_{i=1}^{N}X_i \] は \(N(\mu,\frac{\sigma^2}{N})\) に従う。 \(N\) が大きいということは分散が \(0\) に近づくので、実質 \(\mu\)に収束することを意味する。そして、 \[ Z=\frac{1}{\sqrt{N}\sigma}\sum_{i=1}^{N}(X_i-\mu) \] は \(N\) を大きくしていくと、標準正規分布\(N(0,1)\) に収束する。そこで、多くの場合、母集団からランダムに抽出されたデータは正規分布に従うと仮定することが多い。

標本データから計算される平均や分散などの統計量についての分布を標本分布という。独立に同一の正規分布に従う \(N\) 個の確率変数 \(X_{i}　(i=1,2,\cdots,N)\) について考える。このとき、\(N\)個の2乗和 \(\sum_{1}^{N} X^{2}_{i}\) は自由度\(N\)のカイ2乗分布に従う。カイ２乗分布とは

\[\begin{equation} P(X=x) = f(x,k) = \frac{1}{2^{k/2}\Gamma(k/2)} x^{\frac{k}{2} - 1} e^{\frac{x}{2}} \end{equation}\]

というガンマ関数で表される。この期待値と分散は

\[\begin{eqnarray} E[X] &=& k \\ V[X] &=& 2k \end{eqnarray}\]

である。\(X_i\) から

\[\begin{eqnarray} \hat{\sigma_X^2} &=& \frac{1}{N-1}\sum_{i=1}^N (X_i-\bar{X})^2 \end{eqnarray}\]

を分散\(\sigma\) の推定値とすると

\[\begin{eqnarray} \chi^2 &=& \frac{(N-1) \hat{\sigma_X^2} }{\sigma^2} \end{eqnarray}\]

は自由度\(N-1\) のカイ2乗分布に従う。そこから信頼区間などを計算することができる。また、\(Z\)が正規分布\(N(0,1)\)、Wが自由度\(m\)のカイ２乗分布に従うとすると \[ T= \frac{Z}{\sqrt{W/m}} \] は t分布に従う。t分布は

\[\begin{eqnarray} f(t) &=& \frac{\Gamma(\frac{m}{2})}{\sqrt{(m-1)\pi} \Gamma(\frac{m}{2}} \left( 1+\frac{t^2}{m-1} \right) ^{\frac{m}{2}} \end{eqnarray}\]

とかけ、期待値と分散は \(m >3\) のとき

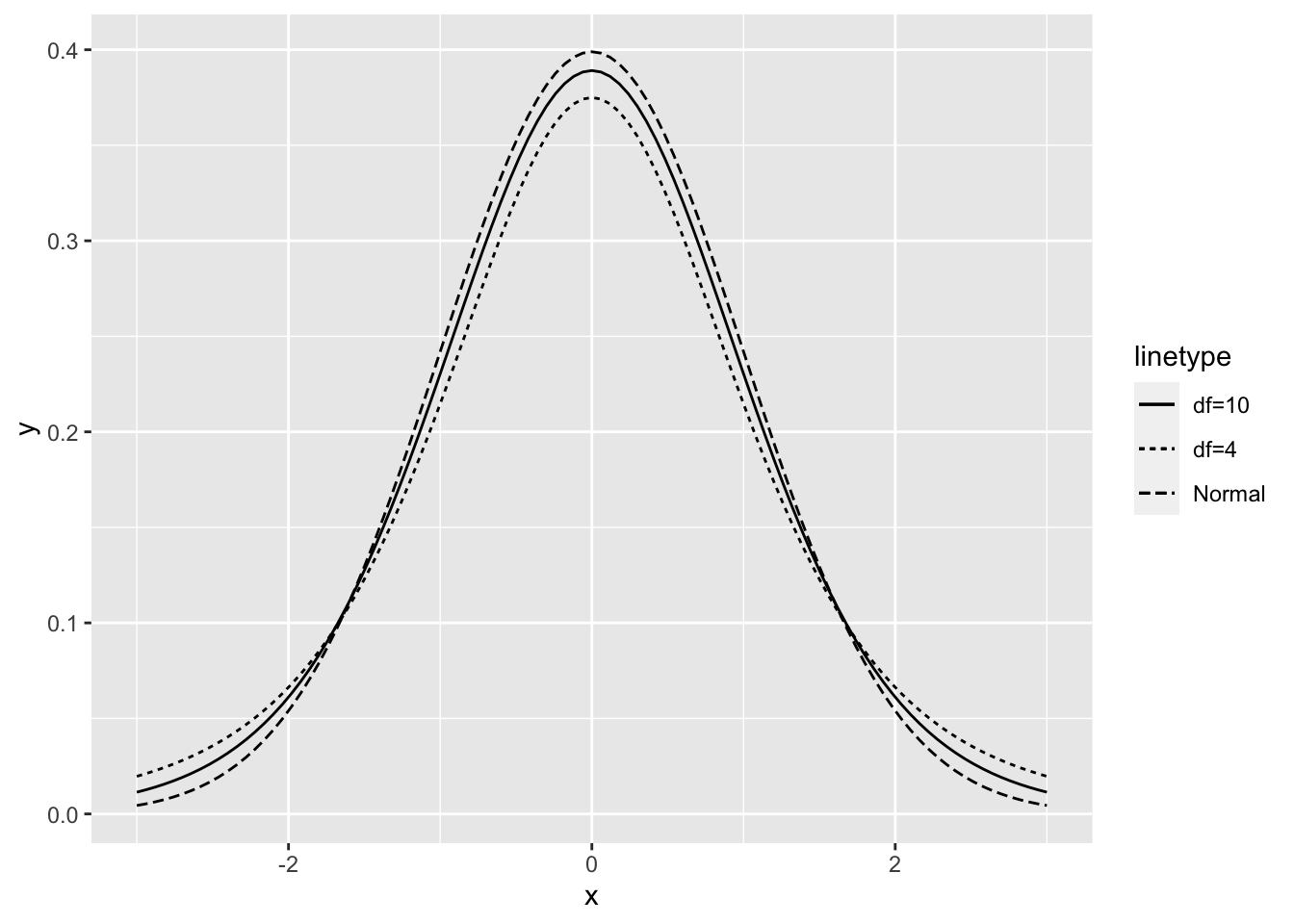
\[\begin{eqnarray} E[T] &=& 0　\\ V[T] &=& \frac{m}{m-2} \end{eqnarray}\]

となる。そこで、\(Z=\frac{\sqrt{N}(\bar{X}-\mu)}{\sigma}\)、 \(W\)を\(\chi^2\)、\(m=N-1\) として、最終的に求まる \[ T = \frac{\sqrt{N}(\bar{X}-\mu)}{\hat{\sigma_X}} \] は自由度 \(N-1\) のt分布に従う。分布は、母分散が未知の正規分布に従う場合の母平均の検定などに用いられる。正規分布に比べると少し幅が広く、\(N\)が大きくなると正規分布に近い形になっていく。また、対応のある2つの母集団における平均の検定など（t検定）に用いられる。

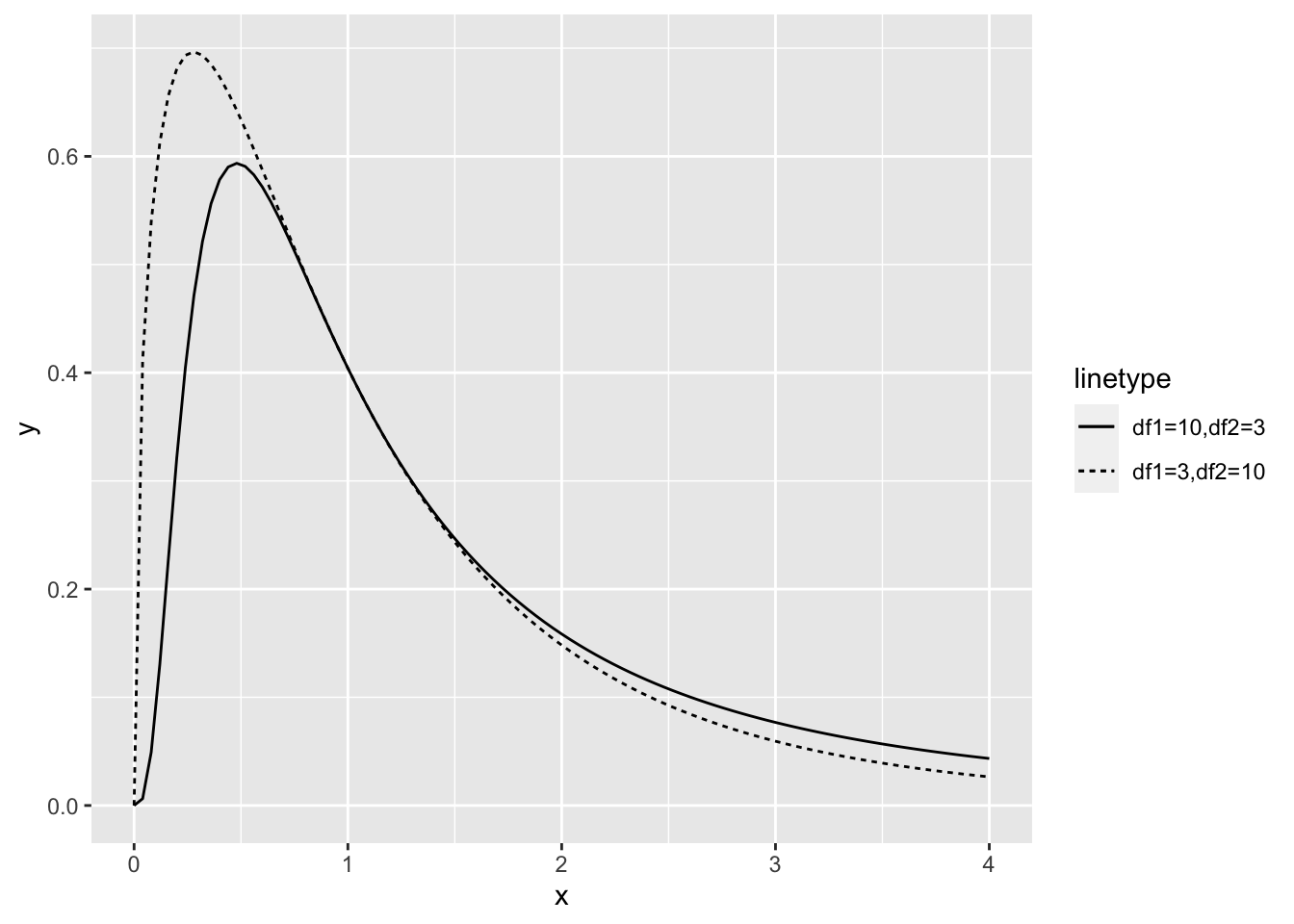
最後に、自由度 \(M\)、\(N\) の2つのカイ2乗分布から取り出したデータ \(U_M\)、\(V_N\) から作られる 2つの値 \({U_M}/{M}\) と \({V_N}/{N}\) の比は自由度 \(M\)、\(N\) のF分布に従う。どちらが分母であるかによって F値は異なるも。グラフでも df1、df2を入れ替えるとグラフの形も異なる。

それぞれ異なる正規分布\(N(\mu_1,\sigma_1)\)、\(N(\mu_2,\sigma_2)\) に従う \(2\) つの母集団から、それぞれ \(M\) 個、\(N\) 個のデータ \(x_i\) \((i=1,2,\cdots,M)\)、\(y_j\) \((j=1,2,\cdots,N)\) を取り出した時、

\[\begin{eqnarray} \bar{x} &=& \frac{1}{M} \sum_{i=1}^{M}x_i \\ \bar{y} &=& \frac{1}{N} \sum_{i=1}^{N}y_j \end{eqnarray}\]

として、

\[\begin{eqnarray} \hat{\sigma_{X}}^2 &=& \frac{1}{M-1} \sum_{i=1}^{M}(X_i-\bar{X})^2 \\ \hat{\sigma_{Y}}^2 &=& \frac{1}{N-1} \sum_{j=1}^{N}(Y_j-\bar{Y})^2 \end{eqnarray}\]

を求めると、 \(\hat{\sigma_{X}}^2\)、 \(\hat{\sigma_{Y}}^2\) はそれぞれ自由度 \(M-1\)、\(N-1\) のカイ2乗分布にしたがう。そして、

\[\begin{eqnarray} F &=& \frac{ \frac{\hat{\sigma_{X}^2 }}{\sigma_1^2} } {\frac{\hat{\sigma_{Y}^2} }{\sigma_2^2} } \\ &=& \frac{\hat{\sigma_{X}^2} \sigma_2^2 } {\hat{\sigma_{Y}^2} \sigma_1^2 } \end{eqnarray}\]

は自由度 \(M-1\)、\(N-1\) のF分布に従う。 2群のデータの平均が等しいかどうかという場合などのF検定で用いられる。これを R でシミュレーションしてみよう。分散の異なる正規分布から、それぞれ、 \(M\)個、\(N\)個の乱数を発生させて、 F値を計算する。これを trial回繰り返し行いヒストグラムを書いてみる。先ほどの説明によればこれはF分布に従う。 geom_histogram において y=after_stat(density) とすると度数ではなく、割合に変換して表示してくれる。

> library(tibble)
> trial <- 2000
> sigma1 <- 2
> sigma2 <- 3
> M <- 53
> N <- 67
> a <- vector("numeric",length=M)
> for(i in 1:trial){
+   x <- rnorm(M,0,sigma1)
+   y<- rnorm(N,0,sigma2)
+   S_1 <- sum((x - mean(x) )^2)/(M-1)
+   S_2 <- sum((y - mean(y) )^2)/(N-1)
+   a[i] <-  (S_1 / sigma1^2) / (S_2 /sigma2^2) 
+ } 
> df1 <-tibble(x=a)
> ggplot(data=df1,aes(x=x))+geom_histogram(aes(y=after_stat(density) ),
+                                          bins=50 )+
+   geom_function(data=data.frame(x=c(0,2) ),aes(x=x),
+                 fun =df,args=c(df1=M-1,df2=N-1),linetype="dotted")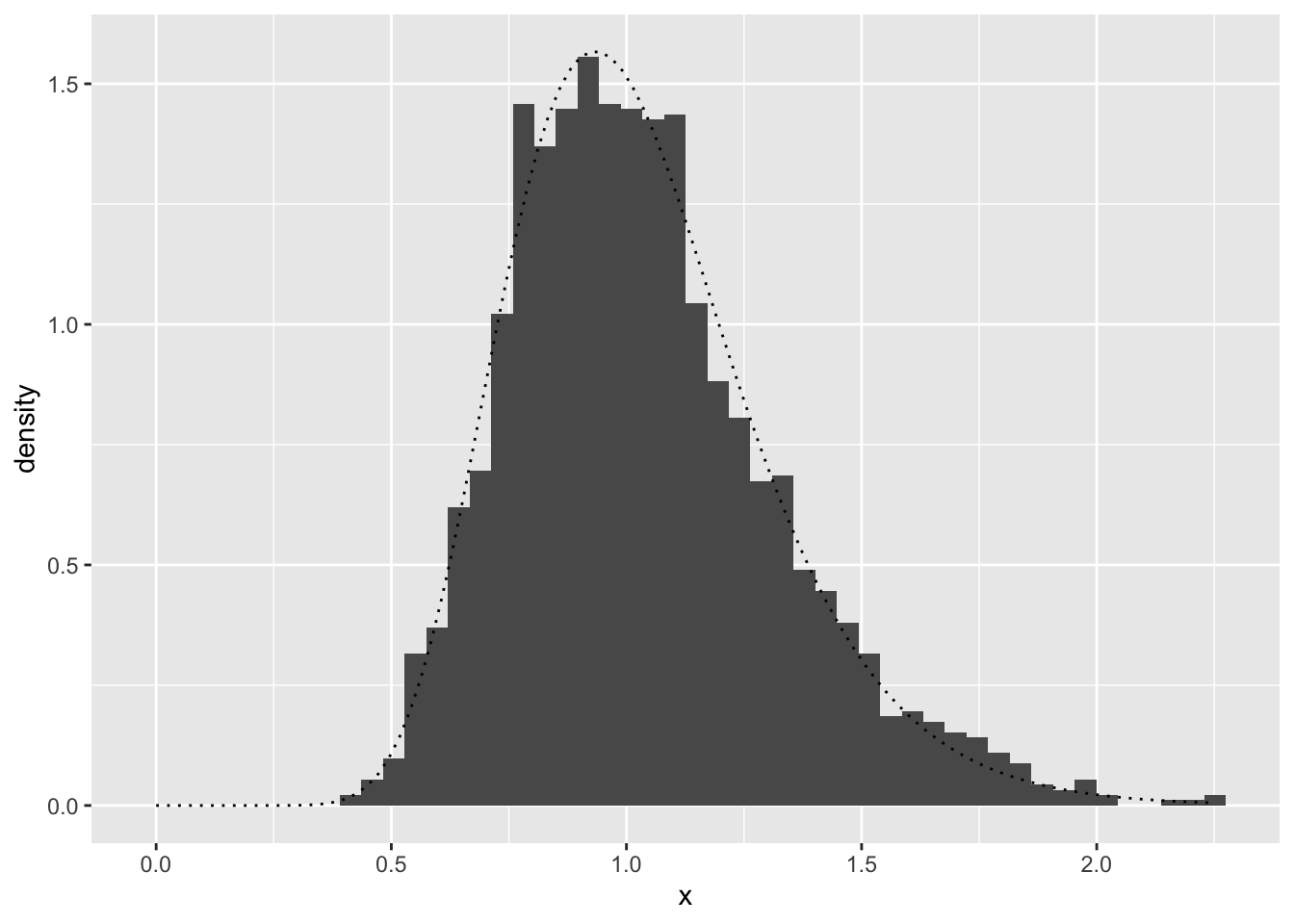

F分布の理論値とよくうまく重なっていることがわかる。 R ではデータフレームがよく使われ、変数として df を使うことが多いが、もし使っていると、関数を描画するときに fun=df がうまく描画されないので注意する。

5.5 乱数

Rでは乱数を発生させる関数があるが、コンピュータはサイコロを振るわけではなく、最初に乱数の種（seed）の値を定め、そこからある手順（この計算の手順をアルゴリズムという）に従い計算して値を求めている。こうした乱数の持つ性質については古くから研究がされている。したがって、自分で実装するよりは、あらかじめ用意された関数を使うのが良い。これから説明する手法の中には、乱数を用いることがある。毎回結果が異なるのではなく、同じ結果を再現したいということがある。乱数は元となる種の値をもとに計算されるため、同じ種から発生させた乱数は同じ値となる。種の値を定めるには、set.seed とする。runif(N,min,max) とすると区間\([{\rm min},{\rm max} ]\)の間の一様乱数を \(N\) 個出力する。結果を見てみよう。

> runif(1,0,1)

[1] 0.426067

> runif(1,0,1)

[1] 0.5536685

> set.seed(0) 
> runif(1,0,1)

[1] 0.8966972

> set.seed(0) 
> runif(1,0,1)

[1] 0.8966972

このように同じ値となっていることがわかる。

5.6 ファクター

Rで扱うデータの型として文字列や数値型、真理値などの論理値の他にファクター(factor)という型がある。次のような例を考えてみよう。

> size1 <- c("S","M","L","M","XL","S","L") 
> size1

[1] "S"  "M"  "L"  "M"  "XL" "S"  "L"

> str(size1)

 chr [1:7] "S" "M" "L" "M" "XL" "S" "L"

この7個の要素からなるベクトルは服のサイズのように4種類の値を持つ。今後扱うデータによっては、限られた種類の中の何かであるということがわかった方がよいこともある。このような場合には factor()という関数を使うと、水準（Level）と呼ばれる値を追加しデータをカテゴリーに分類する。

> size2  <- factor(size1)
> size2

[1] S  M  L  M  XL S  L 
Levels: L M S XL

水準は内部では数値として扱われる。この例ではアルファベット順となっており、服のサイズの順にはなっていない。自分では明示的に指定するには levels とする。

> size3 <- factor(size1,levels=c("S","M","L","XL")) 
> str(size3)

 Factor w/ 4 levels "S","M","L","XL": 1 2 3 2 4 1 3

ファクター型のオブジェクトに対して、関数table()を用いると水準ごとに集計した1次元の表が得られる。データの要約結果を示すsummary()という関数を用いても同様の結果が得られる。年齢や試験の点数のような数値データを、ある階級に分けたいという場合もある。カテゴリー分けをする場合にはcut()という関数がある。階級を \(n\) 個に分けるには (\(x_0\) 〜 \(x_1\)、\(x_1\) 〜 \(x_2\)、\(\cdots\)、\(x_{n-1}\) 〜 \(x_n\) ）と \(n+1\)個の値が必要で、これを breaks=c() の中に順に指定する。また、\(a\) から \(b\) までの区間で区切る場合には \(a < x \leqq b\) 、\(a \leqq x < b\) の場合が考えられる。 cut は何も指定しない場合には前者に相当する right=T が既定値となる。変更するには right=F とする。また、前者の例で、もし \(x=a\) の場合にはどの区間にも入らないことになってしまう。そこで、次の例では前者の場合には一番小さい値よりも 1 小さいものから始め、後者の場合には最大値より 1 大きい値を指定している。３番目の人が上としたで違うラベルに階級に分けられている。

> age1 <- c(10,26,30,48,60)
> m1 <- min(age1)
> m2 <- max(age1)
> cut(age1,breaks=c(m1-1, 30, m2), 
+     label=c("N","Y"))

[1] N N N Y Y
Levels: N Y

> cut(age1,breaks=c(m1, 30,m2+1), 
+     right=F, label=c("N","Y") )

[1] N N Y Y Y
Levels: N Y

5.7 まとめ

他の確率分布との関連づけながら代表的な確率分布について説明した。中には複雑な形をしているものもあるが、その特性については古くから多くの研究がされているのでその結果を利用すれば良い。正規分布から派生した標本分布は統計的仮説検定でよく用いられる。 Rを利用すると、多くの乱数を生成することもできる。たとえば、ある分布からヒストグラムを計算し、実際の理論グラフと比較するといったことができ、確率分布についてのイメージを深めることができる。検定などを含めた統計のテキストとしては参考文献の [1] がコンパクトにまとまっている。

参考文献

[1 ]. 日本統計学会,“統計学基礎 : 日本統計学会公式認定統計検定2級対応”, “東京図書”,2021

[2]. 平岡和幸,堀玄,“プログラミングのための確率統計”, オーム社,2009

[3]. 林賢一,下平英寿,Rで学ぶ統計的データ解析,講談社,2020

演習

ポアソン分布の平均と分散が\(\lambda\) であった。

> set.seed(0)
> N <- 100
> lambda <- 3
> x <-  rpois(N,lambda)
> mean(x)

[1] 3.07

> var(x)

[1] 2.18697

として確認できる。Nを変えて試してみよう。 N を大きくするとlambdaに近づくことが確認できる。また、これを. trial回数だけ和を計算してヒストグラムを書いてみるとそれぞれの広がり方を確認できる。

> set.seed(0)
> N <- 40
> lambda <- 3
> trial <- 300
> a <- vector("numeric",length=trial)
> b <- vector("numeric",length=trial)
> c <- vector("numeric",length=trial)
> for(i in 1:trial){
+   a[i] <-  sum( rpois(N,lambda) - lambda)
+   b[i] <-  a[i]/sqrt(N)
+   c[i] <-  a[i]/N
+ }
> ggplot()+geom_histogram(aes(x=a),bins=30)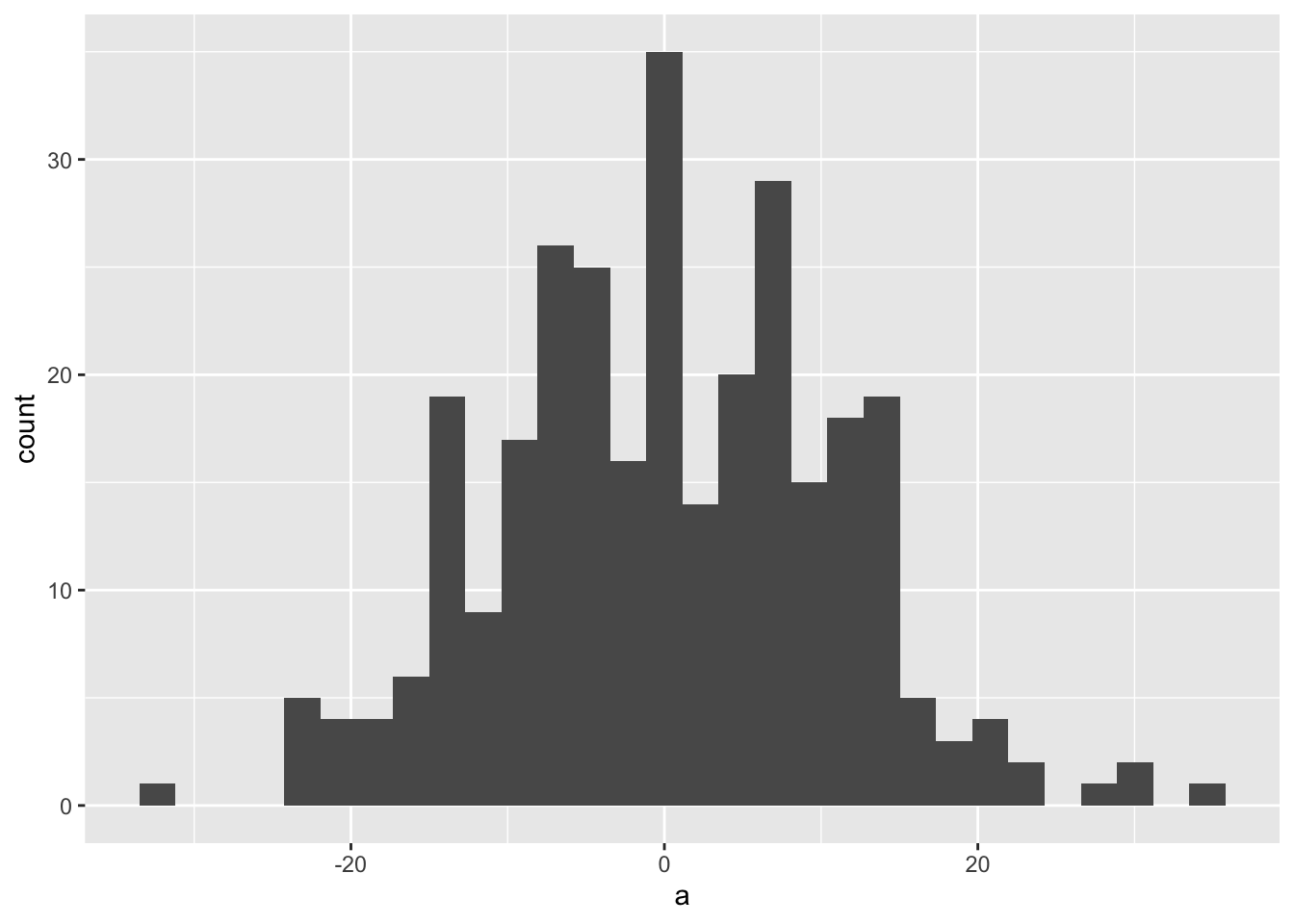

> ggplot()+ geom_histogram(aes(x=b),bins=30)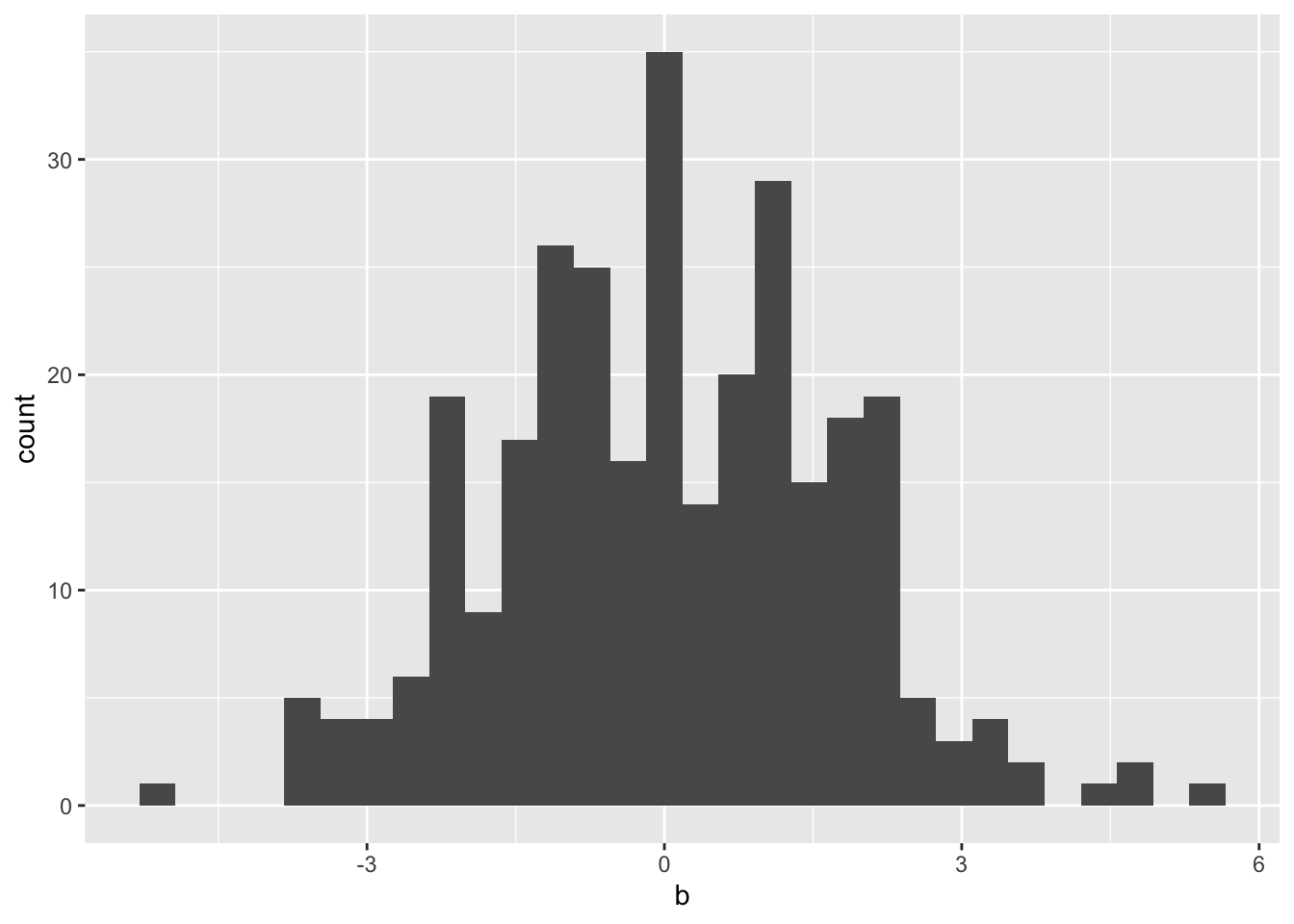

> ggplot()+ geom_histogram(aes(x=c),bins=30)