得られたデータの値を予測するというだけでなく データからなぜそのような結果になったのかという、 データに潜む要因を知りたいということもある。こうした 因子分析について述べる。 因子分析の概要、および因子負荷量の計算について説明する。
因子分析、因子負荷量、カイザーガットマン基準、 因子の回転
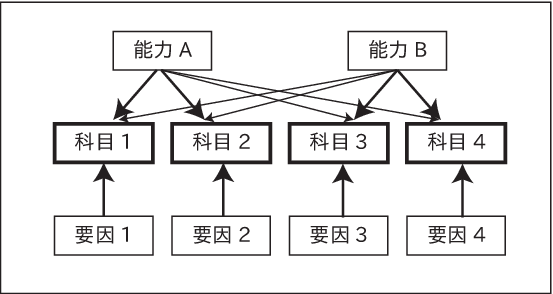
試験によってその人の学力を推測しようとしても、 限られた方法で測定することは難しい。個人の持っている学力というものは 測定しづらいが、 何らかの方法で学力というものが定量化されるものだとしよう。 そうだとして、同じ学力を持つ人は毎回同じ点数を得られるだろうか。 ちょっとしたミスやそのときの体調が結果に影響を与えるかもしれない。 また、複数の科目があるとしよう。理系科目が得意な人や文系科目が得意な人もいる。 国語や社会の点数が高いことから、文系科目が得意な人だと判断したり、そうした人は 数学や理科が苦手だと判断したりすることもある。 こうしたことは科目の点数から、その人の学習に対する態度や能力を推測しようとしていると 考えることもできる。
科目の得点に相当するものを \(Y_j\) \((j=1,2,\cdots n)\) とし その得点の要因となるものを \(n\) よりも少ない \(m\) 個の要素 \(F_k\) \((k=1,2,\cdots m)\) の線形結合によって表すことを考える。 また、それ以外にも個々の科目にはそれぞれに特有の要因 \(E_j(j=1,2,\cdots n)\) があるとする。すると
\[\begin{eqnarray} \nonumber Y_1 &=& c_{11}F_1+c_{12}F_2+\cdots+ c_{1m}F_m +d_1E_1 \\ \nonumber Y_2 &=& c_{21}F_1+c_{22}F_2+\cdots+ c_{2m}F_m +d_2E_2 \\ \nonumber &\vdots& \\ \nonumber Y_n&=& c_{n1}F_1+c_{n2}F_2+\cdots+ c_{nm}F_m + d_mE_m \end{eqnarray}\]となる。これは行列で書くと \[ \boldsymbol{Y} = C \boldsymbol{F} + D \boldsymbol{E} \tag{13.1}\] と書ける。
この \(F_k\)を 共通因子、 \(E_l\) を独自因子という。 ここで、\(Y_j\)は標準化したデータと考え、平均\(0\)、分散が\(1\)とする。 さらに、\(F_k\)、\(E_k\)について、次のような仮定を置く。
\(F_k\)、\(E_l\)の平均は\(0\)、分散が\(1\)。分散についてはCやDの大きさで調整する。
共通因子\(F_k\)と独自因子\(E_l\)はどれも相関がない。
独自因子はそれぞれの独立で相関がない。
共通因子同士は\(F_k\)と\(F_l\)は相関がある場合とない場合の両方を考える。 相関がない場合を直交解、相関を考える場合を斜交解という。
そこで、この式から \(Y_iY_j\)を計算すると、
\[\begin{eqnarray} Y_iY_j &=& \sum_{k=1}^{m}\sum_{l=1}^{n} c_{ik}c_{jl}F_kF_j +\sum_{k=1}^{m}(c_{ik}d_{i}E_i+c_{jk}d_jE_j)F_k +d_id_jE_iE_k \end{eqnarray}\]となる。この変数について平均を計算すると、左辺は共分散であり、 右辺では上記の仮定から第2項は\(0\)になるので
\[\begin{eqnarray} E[Y_iY_j] = \sum_{k=1}^{m}\sum_{l=1}^{m} c_{ik}c_{jl}E[F_kF_m] +d_id_jE[E_kE_j] \end{eqnarray}\]と計算される。ここで、 \(k = j\)の時のみ、\(E[E_kE_j]=1\)である。 これを、\(E[F_kF_m]=\phi_{km}\) とすると
\[ \Sigma = C \Phi C^T + D^2 \tag{13.2}\] となる。成分を書くと
\[\begin{eqnarray} \nonumber \Sigma &=& \left( \begin{array}{ccc} c_{11} & \cdots & c_{1m}\\ &\vdots&\\ &\vdots&\\ c_{n1} & \cdots & c_{nm}\\ \end{array} \right) \left( \begin{array}{ccc} 1 & \cdots & \phi_{1m} \\ \vdots & \ddots & \vdots \\ \phi_{m1} & \cdots & 1 \\ \end{array} \right) \left( \begin{array}{cccc} c_{11} & \cdots & \cdots & c_{ni} \\ \vdots & \ddots & \ddots &\vdots \\ c_{1m} & \cdots & \cdots & c_{nm} \\ \end{array} \right) + \left( \begin{array}{ccccc} d_1^2 & \cdots & 0\\ \vdots & \ddots & \vdots \\ 0&\cdots & d_n^2\\ \end{array} \right) \end{eqnarray}\]である。 \(Y_{i}\) について観測された \(n\) 個の要素を持つ \(N\) 個のデータ \[ \boldsymbol{y}^{(p)}=(y_1^{(p},y_1^{(p},\cdots,y_n^{(p)}) \] \((p=1,2,\cdots,N)\)から、 この\(C\)、\(\Phi\)、\(D\) を求めるのが因子分析 のプロセスということになる。 計算される \(C\) を共通因子負荷量という。 共通因子に対して直交解を仮定する場合には、 \(\Phi\)は単位行列なので\(C\)、\(D\)のみを求める。 また、式(13.1) のように、\(D^2\)は対角成分だけが\(d_i^2\)であり、 その以外の成分は\(0\)である。 \(n\)個の成分それぞれについて、この\(d_i^2\)の値は、成分独自の影響を表している。この値を独自性と言う。 \(1-d_i^2\)の値は共通因子の影響を足しあわせた値であり、この値を共通性という。
因子分析は、式(13.4) を満たすような\(C\)、\(D\)を見つけ、 式(13.1) のように表すことが目的であるが、 主成分分析とは異なり、因子分析では因子負荷量が一意に決まるわけではない。 例えば、 \(\boldsymbol{F}\)の順番については何も条件がないので、順番についての不定性がある。 また、出来た\(\boldsymbol{F}\)全体をどこかの向きで回転させたとしても条件を満たす。 そこで、様々な仮定のもと因子負荷量の推定値を見つける。 その計算手順は次のようになる。それぞれのステップにおいて様々な方法が提案されているが、ここでは代表的なものとして それぞれ1つずつ説明する。
共通因子の個数\(m\)を定める。
因子負荷量を求める。
因子軸の回転を行う。
結果を解釈する。
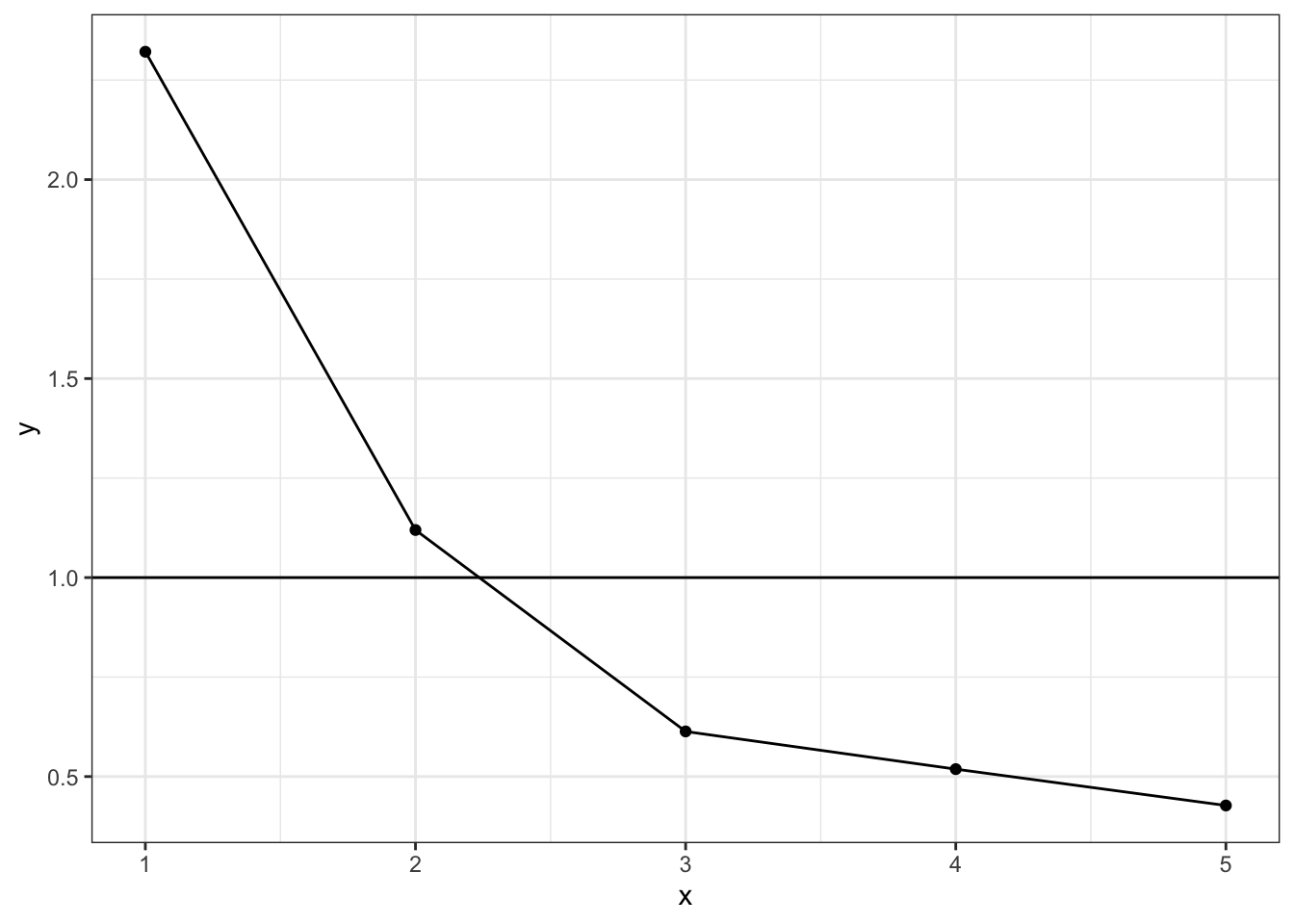
共通因子の個数は予め決まっているわけではない。主成分分析においては相関行列の固有値のもとに累積寄与率を計算した。 相関行列の固有値は必ず \(0\) 以上の値を取った。因子分析でも、固有値の大きさが \(1\) より大きいものに するといった決め方がある(カイザーガットマン規準)。 また、図によって判断する方法もある。 固有値の大きい順に並べ、横軸にその順番を表す番号を取り、縦軸に固有値の大きさを取り プロットする。この図をスクリープロットという。 そして、固有値を成分の影響の大きさと考え、固有値の大きさがあまり変化しなくなる前までの個数を選ぶ。 主成分分析では、\(r\) 次元のデータから\(r \times r\)の相関行列（分散共分散行列）を計算し、その固有値、固有ベクトルを 計算することで主成分を求めた。一方、因子分解では\(n\)個の成分を持つデータを、より少ない\(m\)個の因子で表そうとする。 因子負荷量を求める方法には最尤法、最小２乗法、主因子法といった方法があるが、Rに基本として組み入れられている因子分析factanal()は最尤法を用いて因子負荷量を計算している。\(n\)次元のベクトル\(\boldsymbol{y}^{(p)}\)は互いに独立に多変量正規分布\(N(\boldsymbol{0},\Sigma)\)に従うとすると、データから計算される 相関行列はウィッシャート分布と呼ばれる分布に従う1。 そこから計算される尤度関数を最大にする値として\(C\)、\(D\)が計算される。
\(N\)個のデータから観測されるすべての成分の数は\(n \times N\)個である。一方、\(\boldsymbol{F}\)、\(\boldsymbol{E}\)はそれぞれ \(m \times N\)個、\(n \times N\)個である。これらを直接算出できるわけではなく、データから計算されるのは \(C\)、\(\Phi\)、\(D\)である。 条件を満たすような\(\boldsymbol{F}\)を考え、このFに対して、回転など、大きさを変えず逆変換を持つような線形変換をして\(\boldsymbol{F}^{\prime}\)が得られたとしよう。 それが \[ \boldsymbol{F}^{\prime}= A\boldsymbol{F} \] というように書けるとき、 \[ C\boldsymbol{F} = CA^{-1}\boldsymbol{F}^{\prime} \] であり、 新しく \(A\Phi A^{\prime}\) を \(\Phi^{\prime}\) と考えれば、新しい共通因子を作ることができる。このように、因子分析の解は一意ではない。 そこで、得られた結果をもとに因子の回転を行う。 \(F\)について直交解を仮定した直交回転と斜交解を前提とした斜交回転がある。 回転を行う目的は、特徴をわかりやすく表現することである。 ある判断基準を作成し、(Equation 13.1) にある行列の成分\(c_{ij}\)の値を用いて、 その値が最大になるように負荷量を決定する。 直交回転ではオーソマックス規準が用いられる。オーソマックス規準は
\[\begin{eqnarray} Q &=& \sum_{i=1}{n}\sum_{j=1}{m} c_{ij}^4 \end{eqnarray}\]\(w=1\)の時をバリマックス回転という。 一方斜交回転としてプロマックス回転がある。 あらかじめ目標となる行列を決め、その行列に近づくように因子負荷行列を 変更する方法をプロクラステス回転という。 プロマックス回転は、まずバリマックス解を求める。 バリマックス解の符号はそのままで各成分を\(k\)乗した行列を目標行列として プロクラステス回転を行う。べき乗することで因子間の差が強調され、 因子間の特徴を際立たせることができる。 因子得点\(\boldsymbol{F}\)を推定する方法については省略する。
ここでは、Rに組み込まれているfactanal() という関数を用いて因子分析を行うプロセスを説明する。 手順としては、
データを読み込み、相関行列を計算し因子数を決定する。
因子分析を行う
軸の回転、図示を行い結果を解釈する
という流れで行う。 データは5科目の架空の成績データを用いる。それぞれ、subA からsubE までの計学、神経科学、心理学史、精神分析を架空の試験結果になっている。すでに標準化され、fac01.csvtというファイル名で作業フォルダに置いてあるとする。
> w1 <- read_csv("data/fac01.csv")
> head(w1)# A tibble: 6 × 6
id subA subB subC subD subE
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1 0.822 -0.658 -1.43 0.245 -1.99
2 2 1.14 0.105 0.153 1.22 1.30
3 3 0.185 -0.658 0.153 -0.734 1.30
4 4 -0.453 -1.42 0.680 -0.245 -0.346
5 5 1.46 1.25 -0.375 0.734 1.30
6 6 0.822 0.869 0.153 1.71 -0.346まず、相関行列を計算し、固有値固有ベクトルを計算する。
> w2 <- cor(w1[,-1])
> y <- eigen(w2)$values
> x <- 1:length(y)
> ggplot()+geom_point(aes(x=x,y=y) )+
+ geom_line(aes(x=x,y=y))+
+ geom_hline(yintercept = 1)+theme_bw()
固有値eigen()$valuesは大きい順に並んでいるので、それをプロットする。 このスクリープロットを見ると、3番目から固有値の大きさがあまり変化していない。 また、1より大きい固有値は2つである（カイザーガットマン規準）。 そこで、今回は因子数を2に決定する。 因子分析を行う関数factanal()のパラメータは factanal(データ,因子数,rotation="") rotationとして何もしない（"none"）、バリマックス（"varimax"））、 プロマックス（"promax"））である。 回転として何も選ばないとデフォルトでバリマックスが選択される。 因子数、回転方法を指定して実行する。
> w2 <- factanal(w1[,-1],2,rotation="promax")
> w2
Call:
factanal(x = w1[, -1], factors = 2, rotation = "promax")
Uniquenesses:
subA subB subC subD subE
0.500 0.556 0.526 0.634 0.316
Loadings:
Factor1 Factor2
subA 0.627 0.141
subB 0.728 -0.156
subC 0.637
subD 0.601
subE 0.859
Factor1 Factor2
SS loadings 1.298 1.187
Proportion Var 0.260 0.237
Cumulative Var 0.260 0.497
Factor Correlations:
Factor1 Factor2
Factor1 1.000 -0.488
Factor2 -0.488 1.000
Test of the hypothesis that 2 factors are sufficient.
The chi square statistic is 0.44 on 1 degree of freedom.
The p-value is 0.506 Uniquenessesは独自因子の大きさ\(d_i^2\)を意味している。今回の場合、 共通因子に比べ独自因子が大きい結果になった。共通因子は\(1-d_i^2\)で計算できる。 Loadingsが因子負荷量になる。表示されていない所は\(0\)である。 元のデータが２因子のモデルで表せるという仮説のもとでカイ２乗検定を行っている。 p値が\(0.506\)なので、 ２因子でのモデルは棄却されるほど外れていなかったことを表している。 計算した後に関数varimax()やpromax()を用いることもできる。 出てきた因子をプロットする。
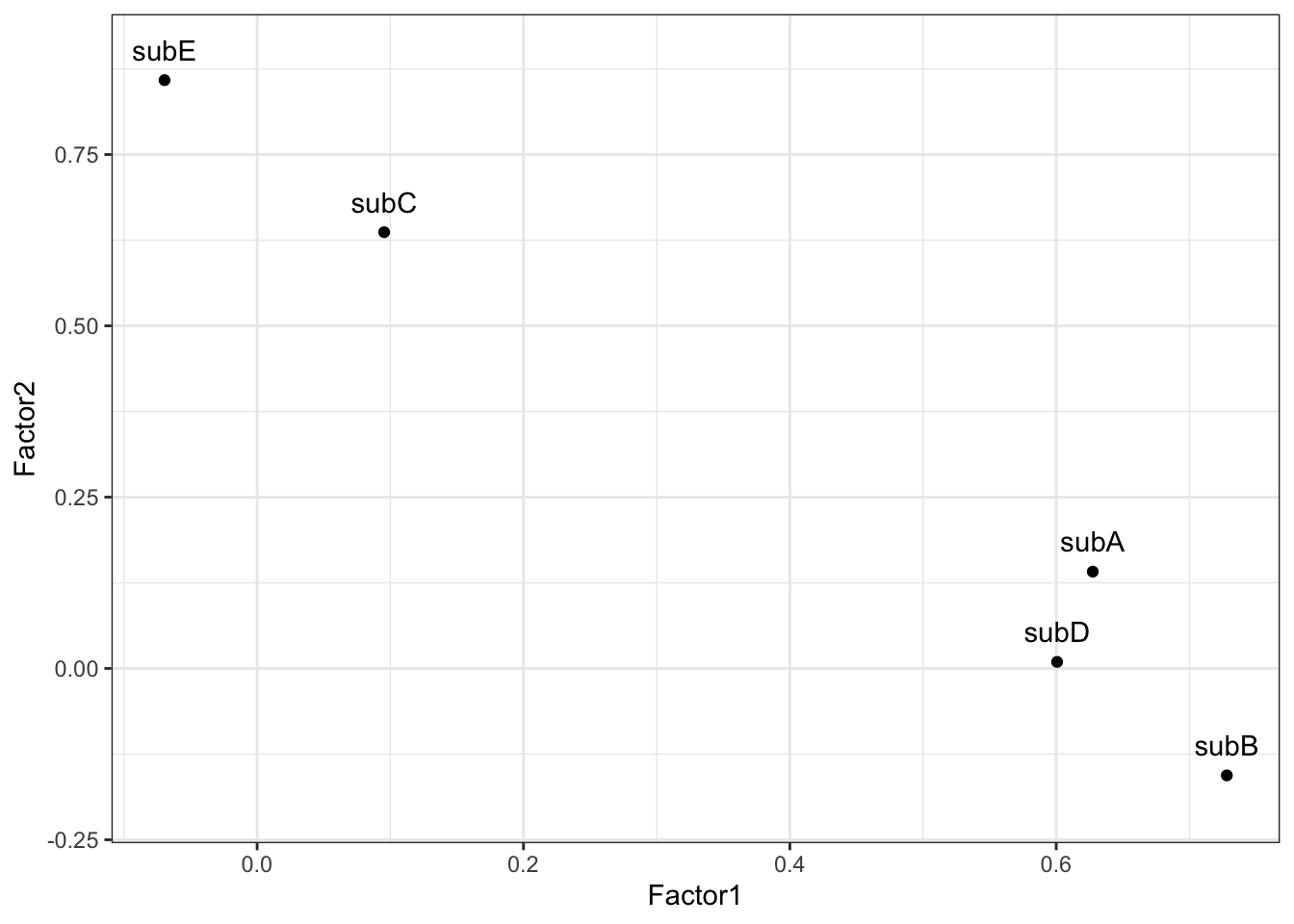
> w3 <- as_tibble(w2$loadings[1:5,1:2])
> w3 <- w3 %>% mutate(subject=rownames(w2$loadings))
> ggplot(w3,aes(x=Factor1,y=Factor2) )+geom_point()+
+ geom_text(aes(label=subject),vjust=-1 )+
+ ylim(-0.2,0.9) + theme_bw()
すると、図1.4のようになる。
これを見ると、5つの科目のうち、3つの科目は因子１が大きく、 2つの科目は因子2 の影響が強いことがわかる。 これより、出てきた結果を図示して、この概念に名前をつける。 因子分析を行う時には、必要な情報として、因子数と根拠、 回転法の情報をまとめておく。
因子分析は主成分分析に似た式であるが、 各要素を生み出す要因となるものを探すという点が異なる。 アンケート調査とは多数の人に同じ質問を用いて調査をすることで 人の行動の背後にある心理や要因を知ろうする。そこでは、 質問を含めた相応しい測定方法が望まれる。こうした尺度を開発しようという 研究も多く行われている。たとえば、長濱らは、 学校でのグループ学習といった協同作業への認識についての尺度開発 を行っている（[1]）。 他にも、田中らは高齢者がどのような基準で 外出する服を選ぶ基準について、19項目の質問項目が 「個人的嗜好」、「流行」、「機能性」、「社会的服装規範」の 4つの因子からなることを示している（[2]）。 そして、安永はこの尺度を用いて20 歳から 79 歳までの 10,800 人に対して調査を行っている。 そして、その4つの因子のスコア（下位尺度得点）を用いて クラスター分析を行い、着装基準のタイプが、 「全基準重視型」、「機能・規範重視型」、 「個人的嗜好・流行重視型」、「無頓着型」の4つに分けられると している（[3]）。
[1]. 長濱文与,安永悟,関田一彦,甲原定房, “協同作業認識尺度の開発”,教育心理学研究, vol. 57(1), pp24-37, 2009
[2]. 田中優,秋山学,泉加代子,上野裕子,西川正之,吉川聡一, “高齢者の自律と着装行動に関する研究―着装基準重視と関連する要因の検討”, 繊維製品消費科学, vol.39(11), pp.716-722, 1998
[3]. 安永明智,“若年者から高齢者における着装基準の類型化と 性, 年代別の特徴”, 繊維製品消費科学,vol.59 (4), pp. 297-303, 2018
[4]. 市川雅教, “因子分析”, 朝倉書店, 2010,
[5] 中村,永友,Rによるデータサイエンス2『多次元データ解析法』, 共立出版,2009
ア 2 イ 5 ウ 2 エ 5 オ 5
多変量正規分布から独立にN個のデータを取り出した時に、 そこから計算される行列 \(\displaystyle{\sum_{p=1}^{N}\boldsymbol{y}^{(p)}(\boldsymbol{y}^{(p)})^T}\)が従う分布を ウィッシャート行列と言い、
\[\begin{eqnarray} \frac{|A|^{\frac{N-n-1}{2}}\exp(-\frac{1}{2}\mathrm{Tr}\Sigma^{-1}A)} {2^{\frac{nN}{2}} \pi^{\frac{n(n-1)}{4}}|\Sigma|^{\frac{N}{2}} \displaystyle{\prod_{i=1}^{n}}\Gamma(\frac{N-i+1}{2}) } \end{eqnarray}\]と表される。\(n=1\)のとき、\(A=x\)、\(\Sigma=1\)であり、カイ2乗分布である。↩︎