15 データの分類

非階層的クラスター分析としてデータを k 個のグループに分ける k 平均法 について説明する。また k 近傍法について説明し、同じ例題を、分類木、ニューラルネットワークの４種類で分類し、その結果について比較を行う。

キーワード

k平均法、k近傍法、混同行列、F値

15.1 k平均法

階層的クラスター分析では各点同士の距離が分かっていればそれを樹形図として表すことができた。しかし、点の数が多い場合に出てくる結果は見にくい。また、クラスターに分類する場合、大体望んだ数のグループに分けることができればよい場合もあるだろう。ここでは、k-means法について述べる。 k-means法とは名前の通り、データを $k$個のクラスターに分ける方法のことをいう。今、全部で $N$個の点があるとし、データの座標が与えられている状況を考える。k-means法でも、実装方法によって細かな違いは多少あるが、例えば次の手順で計算する。

まず $k$個の点をランダムに選び、グループの中心の点であると考える。もしくは、最初に無作為に $k$ 個のグループに分けて、各グループの重心を代表の点にする。ここでは説明を簡単にするため、最初にランダムに $k$個の点を選んだ状態を考える。
残りの$N-k$ 個の点に対して$k$個の代表点との距離を計算し、いちばん近い点のグループに属することにする。これによって、全ての点がとりあえず $k$ 個のグループに分かれることになる。
このようにして作られた $k$個のグループごとにそれぞれの座標から重心の点の座標を計算し、その重心の点をあらためてグループの中心とする。
全部の点に関してその代表の点との距離を計算し直し、いちばん近いグループに属するようにグループをシャッフルする。

といった手順を繰り返す。最初にグループの中心をどのように決めるか、また決まったグループごとの中心をどのように決めるか、他の点との距離をどのように計算するのかによって、いくつかの種類があるが、基本的な手順は上のようになる。

Table 15.1: 5点の座標
点	$(x,y)$
C1	$(1,1)$
C2	$(2,1)$
C3	$(1,3)$
C4	$(4,5)$
C5	$(5,5)$
C6	$(5,3)$

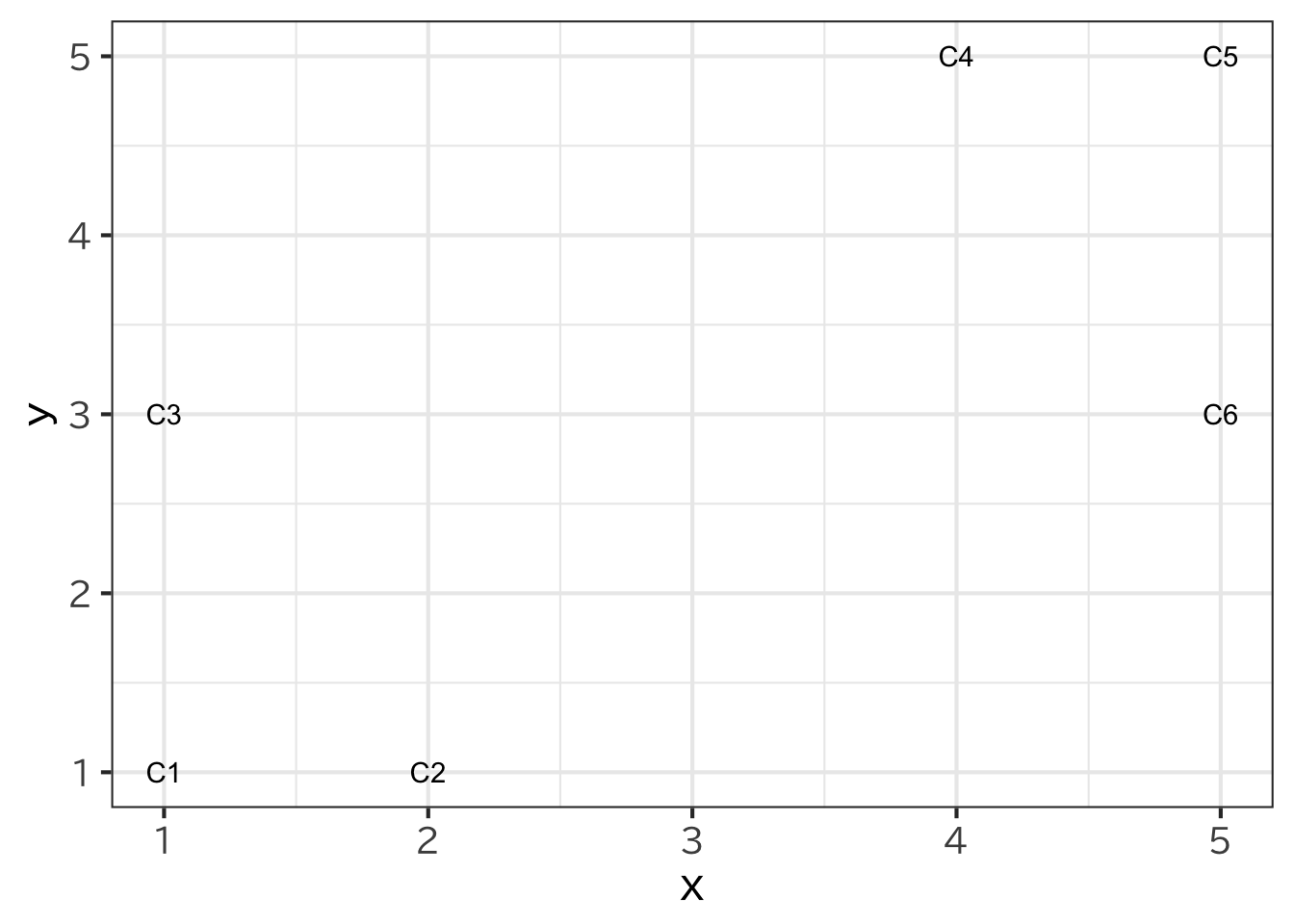
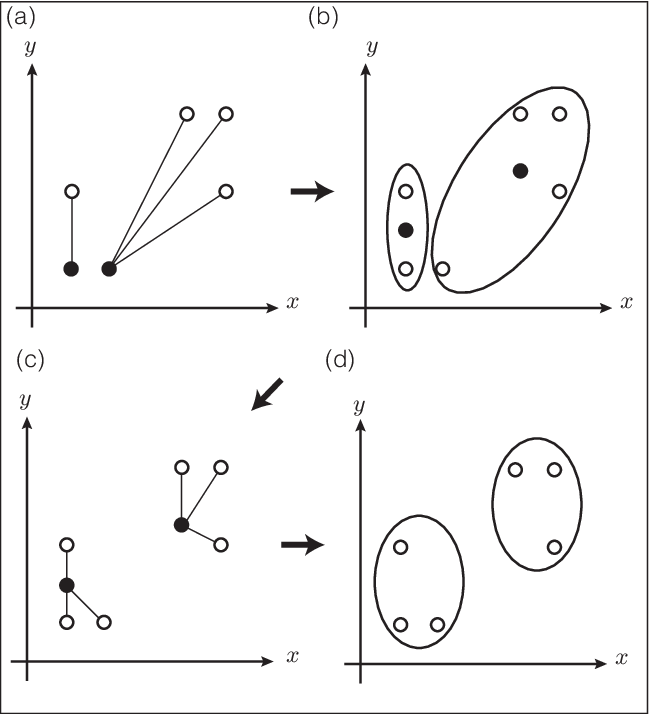
これを例をもとに考えてみよう。6個の点の座標が (Figure 15.1) の表のように与えられているものとする。ここで、各点の距離はユークリッド距離、つまり、2点$(x_1,y_1),(x_2,y_2)$の距離を \[d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}　\] と計算するものとする。これを2つのグループに分けることを考えよう。まず、初期の中心となる点として、C1とC2が選ばれたものとする。すると、C1に近い点としてC3が、C2に近い点としてC4、C5、C6となるから、 2個の点からなるクラスターC1、C3と 4個の点からなるクラスターC2、C4、C5、C6という2つのクラスターに分かれることになる。このように分けることができたら、次にそのクラスターの中心となる点を定める。今、中心の点はクラスター内の点の重心であるとしよう。すると、C1とC3の方であれば、 $\left(\frac{1+1}{2},\frac{1+3}{2}\right)=(1,2)$ 、C2、C4、C5、C6の方が $\left(\frac{2+4+5+5}{4},\frac{1+5+5+3}{4}\right)=(4,3.5)$と求めることができる。そこで、もう一度、この中心点に近い点と遠い点とでグループ分けを行うと最終的に、C1、C2、C3 からなるクラスターとC4、C5、C6 からなるクラスターに分かれる。さらに、これに基づいて計算しても点の入れ代わりがないのでこれで計算が終了となる。この手順を図にすると、 (Figure 15.2) のようになる。

15.2 Rによるシミュレーション

Rでk-means法を使うには、kmeans()という関数を使う。多次元尺度法や階層的クラスター分析の場合には、2点間の距離を入力として与えていたが、kmeans()ではそれぞれの点の座標を入力とする。ω各象限に点$(1,1)$、$(-1,1)$ 、$(-1,-1)$、$(1,-1)$ を中心に標準偏差$\sigma$ として50個の正規乱数を作る。

> library(tidyverse)
> set.seed(38)
> sigma <- 0.25
> ca <- tibble(
+   x=rnorm(50,1,sigma),
+   y=rnorm(50,1,sigma),
+   cl_t="A")
> cb <- tibble(
+   x=rnorm(50,-1,sigma),
+   y=rnorm(50,1,sigma),
+   cl_t="B")
> cc <- tibble(
+   x=rnorm(50,-1,sigma),
+   y=rnorm(50,-1,sigma),
+   cl_t="C")
> cd <- tibble(
+   x=rnorm(50,1,sigma),
+   y=rnorm(50,-1,sigma),
+   cl_t="D")
> t0 <-rbind(ca,cb,cc,cd)
> ggplot(t0,aes(x=x,y=y,color=cl_t))+geom_point()+
+   scale_colour_manual(values=c("gray80","gray40","black","gray60"))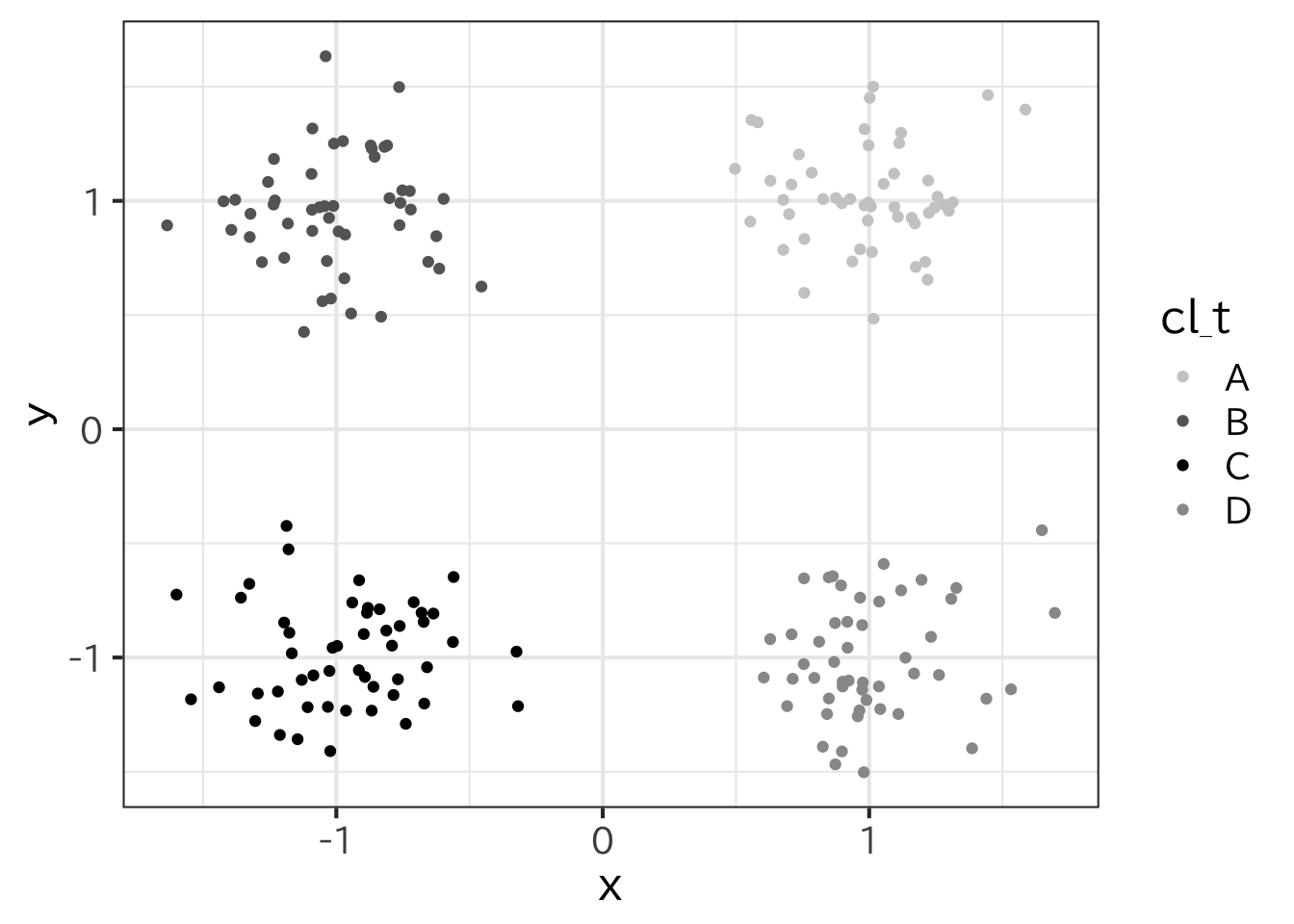

これを kmeans() で分類する。

> k0 <- t0 %>% select(x,y) %>% kmeans(centers = 4)
> k0

K-means clustering with 4 clusters of sizes 50, 50, 50, 50

Cluster means:
           x          y
1 -0.9613972 -0.9855138
2 -1.0002346  0.9525060
3  1.0033236 -1.0075478
4  0.9887441  1.0189317

Clustering vector:
  [1] 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4
 [38] 4 4 4 4 4 4 4 4 4 4 4 4 4 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 [75] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1
[112] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[149] 1 1 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
[186] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3

Within cluster sum of squares by cluster:
[1] 6.416577 6.066010 6.068873 5.382852
 (between_SS / total_SS =  94.2 %)

Available components:

[1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
[6] "betweenss"    "size"         "iter"         "ifault"

この結果の中で、centers が代表点の座標$cluster がクラスターになっている。このとき、全体を1つのグループと見た時の各点と重心との距離は、グループごとの重心との距離と各グループの重心と全体の重心との距離（それにグループの個数を掛けたもの）に分解することができる。そして、全体の重心と各グループの重心との距離の和が示す割合が大きいほど、グループが小さく凝集していると考えることができる。この比率の大きさをうまく分類できているかどうかの指標の1つとしてである。それぞれの値は、全体を1つのグループにした場合のトータルの重心との距離の２乗和(totss)、各グループの重心との全体の重心との距離の２乗和（betweenss）、グループ内での重心との距離の２乗和(withinss)でみることができる。

> k0$totss

[1] 415.9622

> k0$betweenss

[1] 392.0279

> k0$withinss

[1] 6.416577 6.066010 6.068873 5.382852

正しく分類できているかどうかクラスターを元のグループと比較してみる。クラスの名前までは判定できないので、どのクラスターがどのグループかは自分で結果を踏まえて入れ替える。また、k0$cluster は数値の型をしているので　factorにして label のところで入れ替えている。その上で元のグループと分類したグループの表を作成すると

> t0 %<>% mutate(cl_k=factor(k0$cluster,
+                           label=c("A","B","C","D"), 
+                           levels=c(4,2,1,3) ) )
> t0 %>% select(cl_t,cl_k) %>% table()

    cl_k
cl_t  A  B  C  D
   A 50  0  0  0
   B  0 50  0  0
   C  0  0 50  0
   D  0  0  0 50

とうまく分類できていることがわかる。

15.3 k近傍法

分類手法としてシンプルな方法としてk近傍法がある。あらかじめ分類された訓練データがあるときに、訓練データの中で自分と距離の近い$k$個の点の多数決によって分類するというものである。

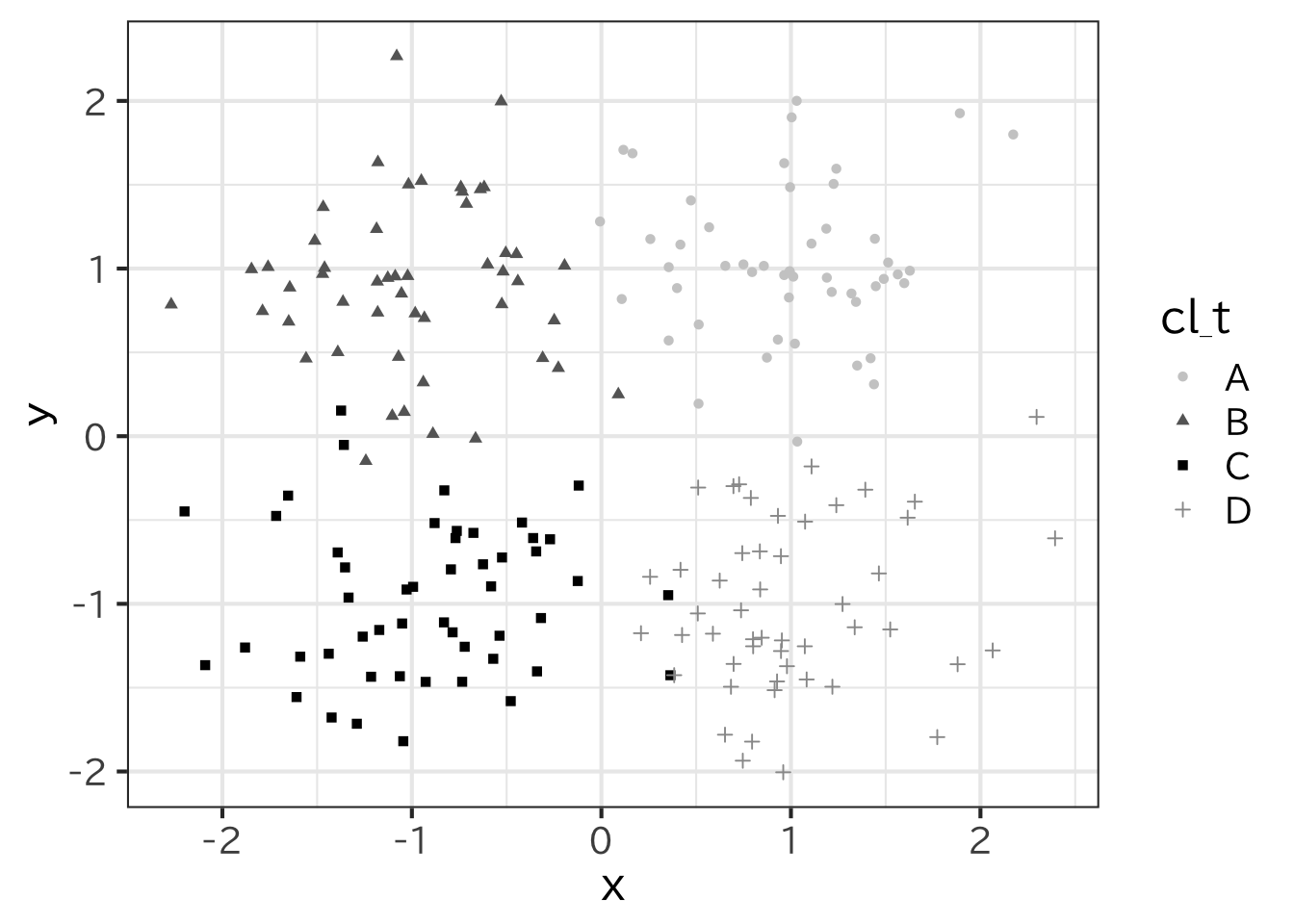
R には class というパッケージに knn() という関数がある。テストデータとして$-2$から$2$ まで等間隔に$N$ 等分する場合、$x$ 座標ごとに$N$個の$y$座標があるので、点の個数は $N^2$個。繰り返しの関数として rep()がある。 rep(1:3,N) とすると 123123$\cdots$ と N 回繰り返し、 each=N は 111$\cdots$222$\cdots$ と各要素をN 回繰り返す。

> min <- -2
> max <-  2
> N_test <- 100
> int<- (max-min) / (N_test-1)
> test　<- tibble( x = rep(seq(min,max,int),each=N_test),
+                  y = rep(seq(min,max,int),N_test) )

knn は訓練データの座標、検証用の座標、訓練データのクラスと近傍の個数$k$ を指定する。

> library(class)
> cl_test <- t0 %>% select(　x　,　y) %>%
+   knn(test, cl=t0$cl_t, k=5)

この結果を図示してみよう。

> ggplot(test,aes(x=x,y=y) )+
+          geom_point(aes(color=cl_test),size=0.5) +
+     scale_colour_manual(
+       values=c("gray80","gray40","black","gray60"))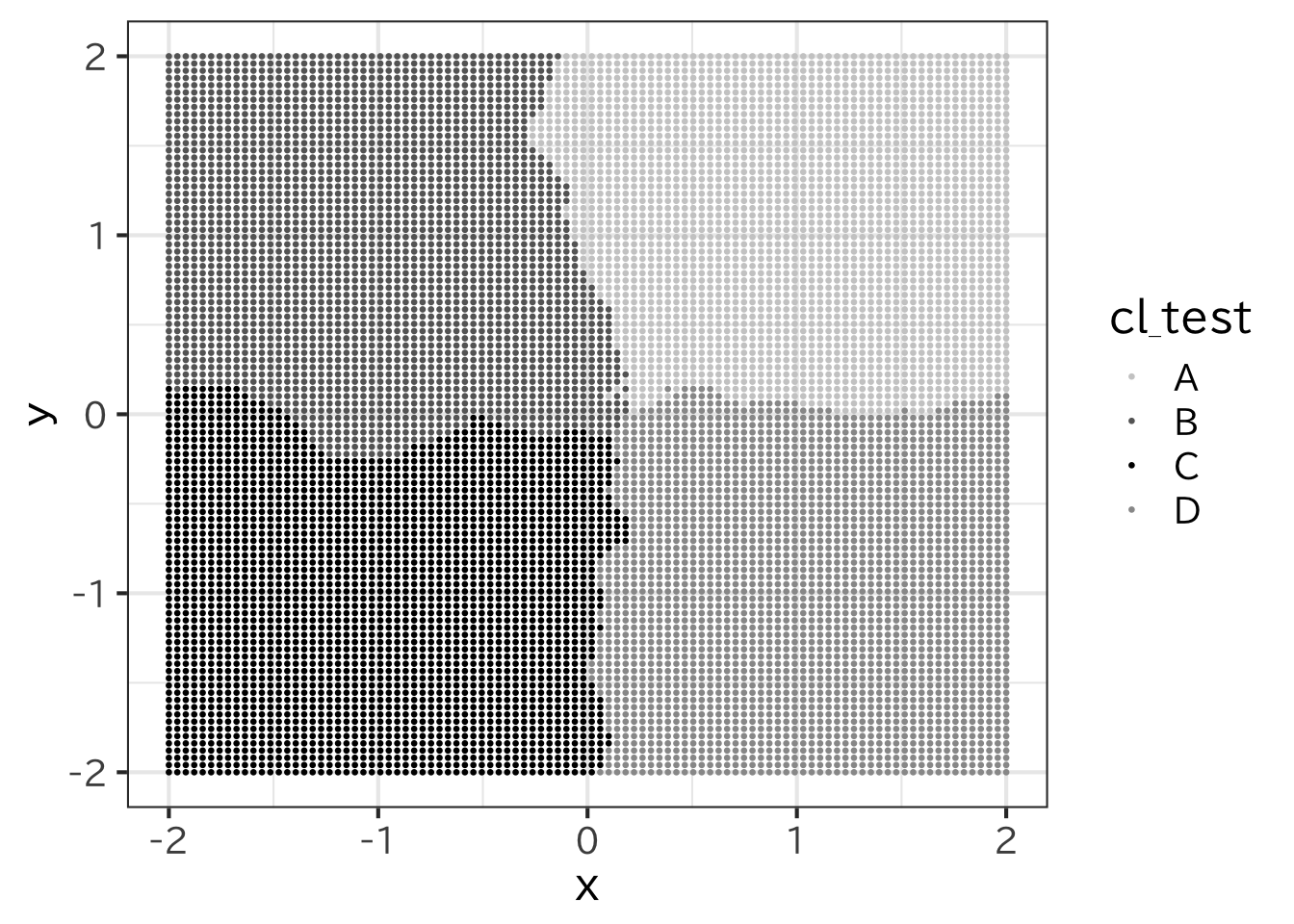

rpart でも分類を行うことができる。

> library(rpart)
> rp_t <- rpart(data=t0, cl_t ~ x + y, method="class")

結果を図示すると

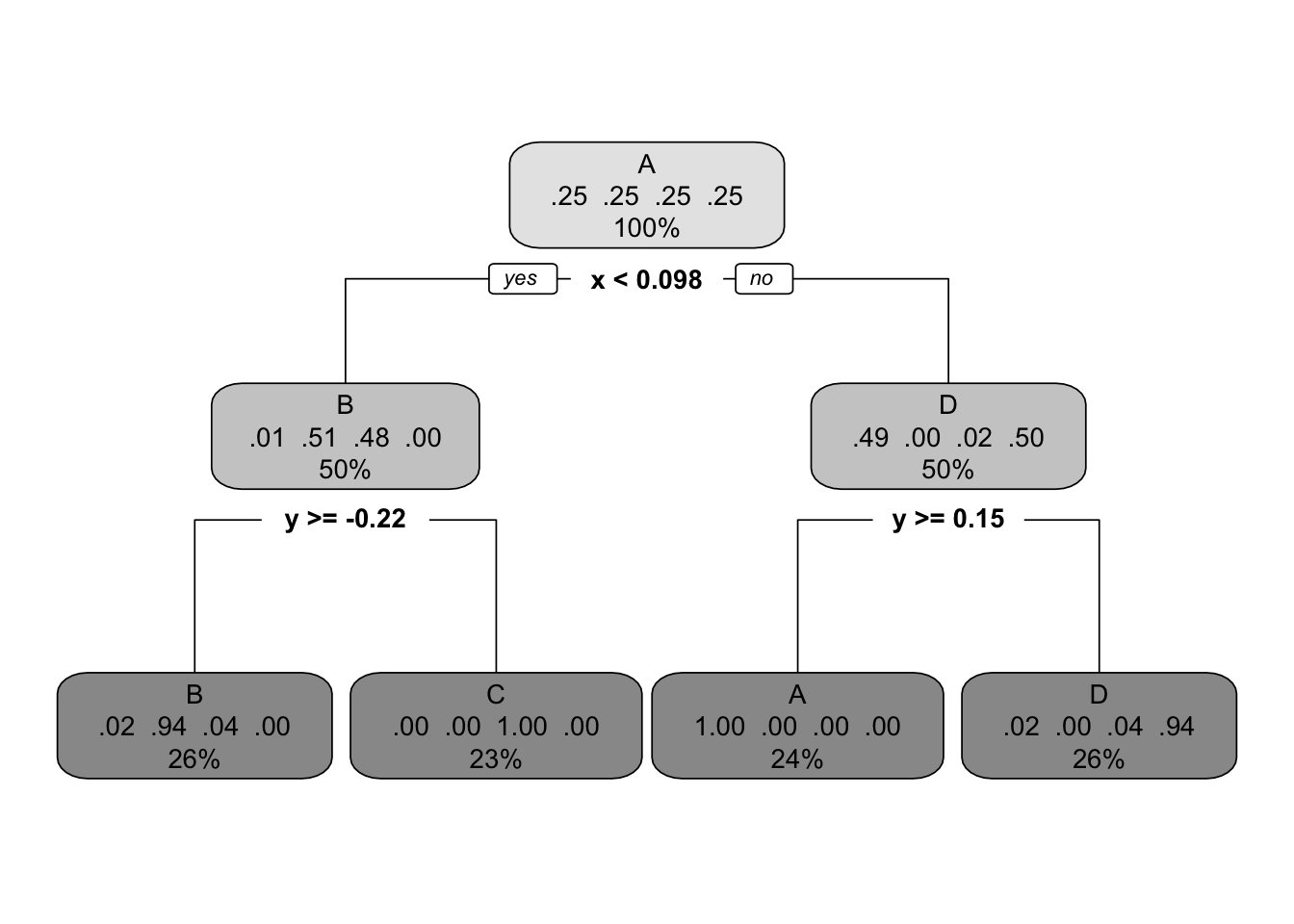
15.4 分類木とニューラルネットワークとの比較

lmと同様に predictとするとテストデータに対して予測を行うことができる。

> rp_test <- predict(rp_t,newdata=test,type="class")

この結果を見てみよう。

> ggplot(test,aes(x=x,y=y)) +
+   geom_point(aes(color=rp_test),size=0.5)+
+   geom_segment(x=rp_t$splits[1,4],y=-2,
+                xend=rp_t$splits[1,4],yend=2)+
+   geom_segment(x=-2,y= rp_t$splits[4,4],
+                xend=rp_t$splits[1,4],yend= rp_t$splits[4,4])+
+   geom_segment(x=2,y=rp_t$splits[7,4],
+                xend=rp_t$splits[1,4],yend=rp_t$splits[7,4])+
+   scale_colour_manual(
+     values=c("gray80","gray40","black","gray60"))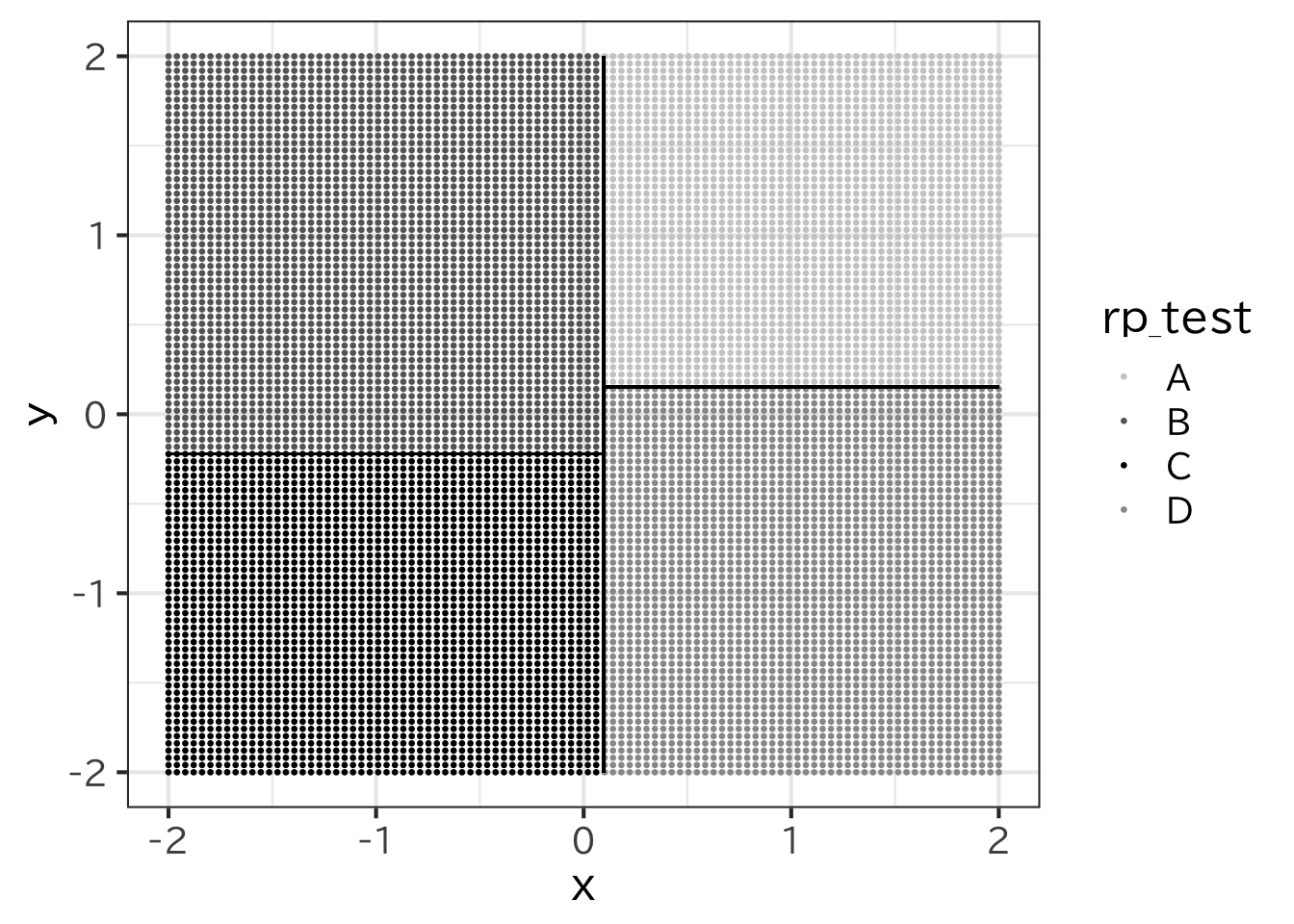

nnetでも分類を行うことができる。nnet ではクラスを文字ではなく因子として与える。出力層に分類するクラス数のニューロンを用意し、該当するクラスのときだけ1を出力する教師信号と捉えて学習を行ってくれる。

> library(nnet)
> t1 <- t0 %>% mutate(cl_t = as.factor(cl_t))
> nn_t <- nnet(data=t1,cl_t~x+y,size=5)

# weights:  39
initial  value 307.902464 
iter  10 value 78.393718
iter  20 value 23.986023
iter  30 value 18.283805
iter  40 value 12.356095
iter  50 value 10.435339
iter  60 value 10.105043
iter  70 value 6.793099
iter  80 value 5.960759
iter  90 value 5.809545
iter 100 value 5.795060
final  value 5.795060 
stopped after 100 iterations

> nn_test <- predict(nn_t,newdata=test,type="class")
> ggplot(test,aes(x=x,y=y)) +geom_point(aes(color=nn_test),size=0.5)+
+    scale_colour_manual(
+      values=c("gray80","gray40","black","gray60"))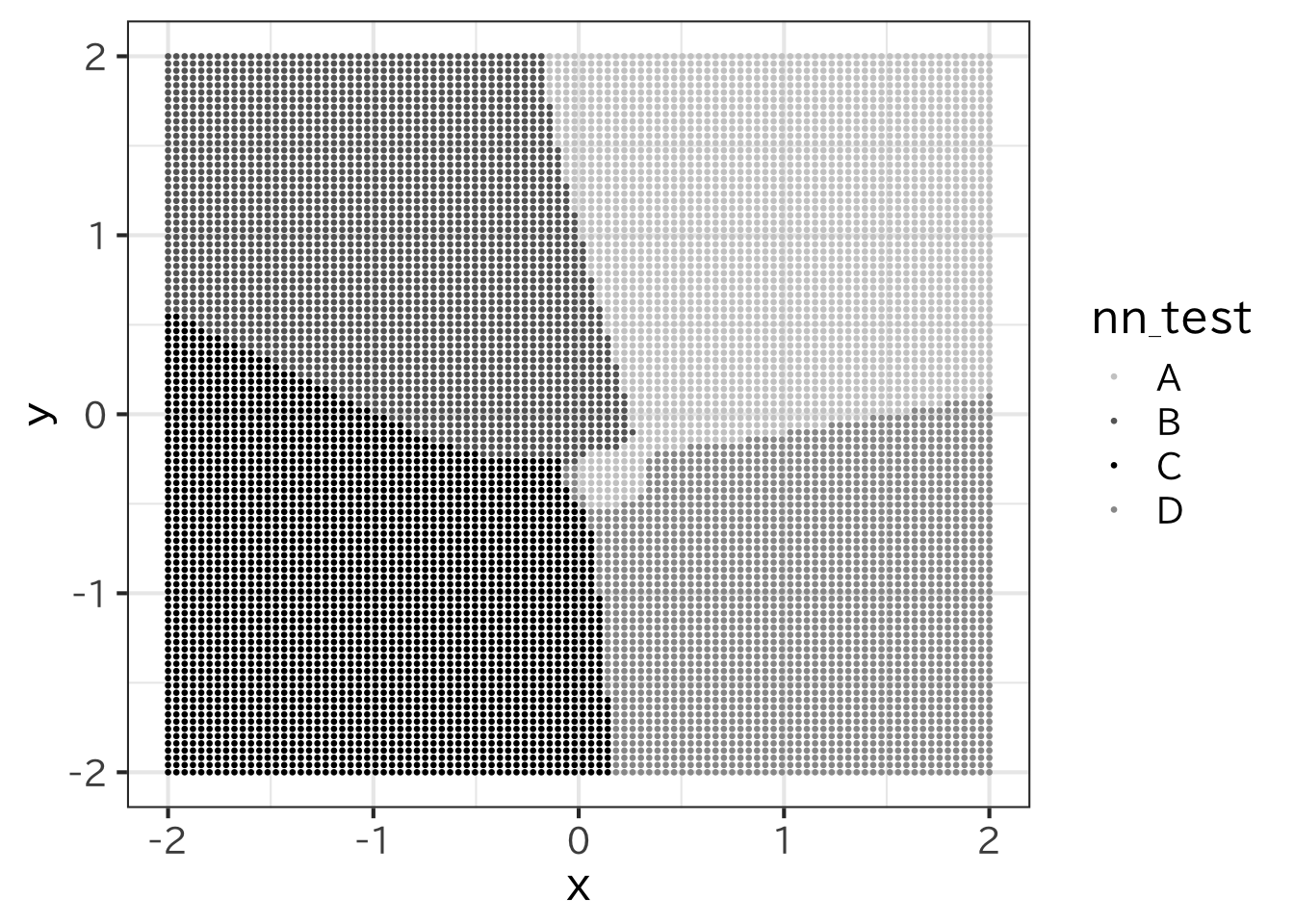

rpartと違い、非線形な線分で場合分けしていることがわかる。

また、分類の評価の正解には、正解がAであるものをAと判定したもの（真陽性)、そうでない(B、C、D)と判定したものを（偽陰性)、正解がAでないものをAと判定したもの（偽陽性)、 Aでないものを正しくAでないと判定したもの(真陰性)、の４種類に分けられる。これを次の表に表したものを混同行列という。

		予測値
		陽性	陰性
真の値	陽性	真陽性(True Positive )	偽陰性(False Negative)
	陰性	偽陽性(False Positive )	真陰性(True Negative)

:分類評価の混同行列 {#tbl-class}

の４種類がある。それぞれを、TP、FN、FP、TNとすると \[ \mbox{正解率(Accuracy) } = \frac{TP+TN}{TP+FP+FN+TN} \] である。たとえば銀行での本人確認を行うという場合には何度かやり直しても良いので、他人を間違えて本人として欲しくない。この場合には FPを減らしたい。その時には高い適合率を用いる。 \[ \mbox{適合率(Precision) } = \frac{TP}{TP+FP} \] 一方、病気の判定という場合、病気でないのに病気と判定されても再検査をすればよいが、病気を見逃しては困るという場合には FNはなるべく減らしたい。このような場合には高い再現率が求められる。 \[ \mbox{再現率(Recall) } = \frac{TP}{TP+FN} \] 適合率と再現率の調和平均を取ったF値 (F-measure,F-score)を評価基準として用いることもある。

\[ \mbox{F値 (F-measure) } = \frac{2}{ \frac{1}{\mbox{Precision}　}+\frac{1}{\mbox{Recall} }　} =\frac{2(\mbox{Precision}\cdot\mbox{Recall} )}{ \mbox{Precision}+\mbox{Recall} } \]

15.5 まとめと展望

グループに分ける方法についてさまざまな手法を主に例題をもとに説明した。コンピュータは単純作業が得意である。繰り返し作業は人よりも速く確実に行ってくれる。ツールが充実し、容易にデータ分析を行うことができるようになった。そこで、分類手法にどのような特徴があるのかを比較を通してみた。紹介しきれなかった手法も多くある。それについては各章に載せた参考文献を参照してほしい。

参考文献

[1]. 林賢一,下平英寿,Rで学ぶ統計的データ解析,講談社,2020

[2]. Trevor Hastie,Robert Tibshirani,Jerome Friedman（著）, 杉山将,井手剛,神嶌敏弘,栗田多喜夫,前田英作（訳）, “統計的学習の基礎 : データマイニング・推論・予測”, 共立出版,2014,https://hastie.su.domains/ElemStatLearn/

[3]. 金明哲,“R によるデータサイエンス(第2版)”,森北出版,2017

演習

k 近傍法では近隣の個数 k を変えると振る舞いが変わる。 k が大きくなれば変化に鈍く、小さければ敏感になる。そのため小さいとノイズの影響を受ける。そのことを試すと次のようになる。

> cl2_test <- t0 %>% select(x,　y) %>%
+   knn(test,　cl = t0$cl_t, k=2)
> ggplot(test,aes(x = x,　y = y) )+
+          geom_point(aes(color = cl2_test ), size=0.5) +
+   scale_colour_manual(values=c("gray80","gray40","black","gray60"))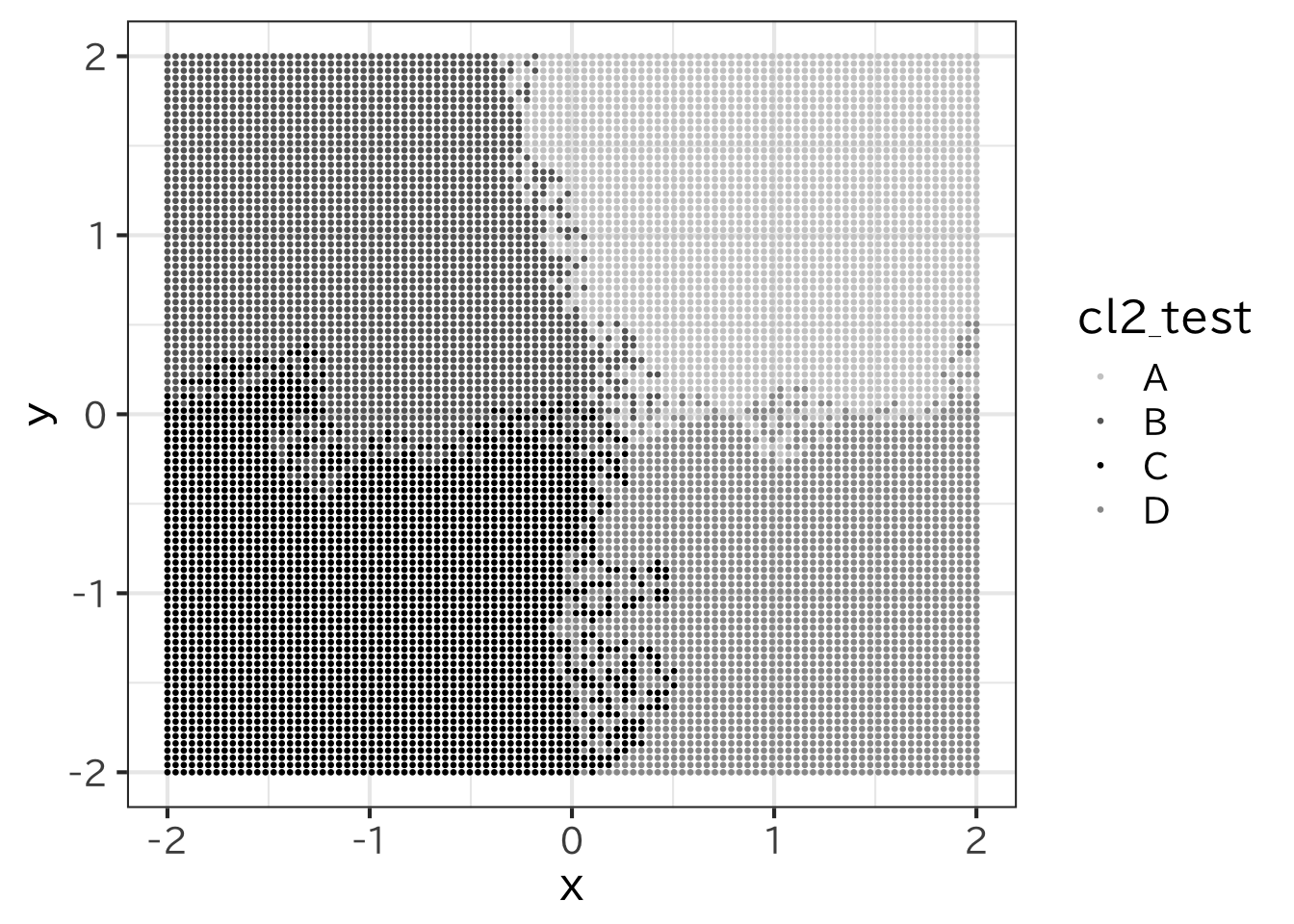

2.後半は検証用の方に正解を入れていなかったが、検証用のデータのサイズは N_test*N_test個あり、４等分の正解がある。

> M <- N_test^2 / 4 
> test_a <- test %>% 
+   mutate(true = ifelse(x > 0,ifelse(y>0,"A","D"),
+                        ifelse(y>0,"B","C") ) ) %>%
+   mutate(true = factor(true))
> test_a %<>% mutate(cl_t=cl_test, 
+                    rp_t=rp_test,nn_t=nn_test)
> test_a %>% select(true,cl_t) %>% table()

    cl_t
true    A    B    C    D
   A 2371   60    0   69
   B  113 2343   44    0
   C    0  119 2381    0
   D    0   11  102 2387

> test_a %>% select(true,rp_t) %>% table()

    rp_t
true    A    B    C    D
   A 2208  100    0  192
   B    0 2500    0    0
   C    0  250 2250    0
   D    0   10   90 2400

> test_a %>% select(true,nn_t) %>% table()

    nn_t
true    A    B    C    D
   A 2404   79    0   17
   B   60 2252  188    0
   C    0  111 2381    8
   D  151   31  107 2211

diag　は行列の対角成分だけを取り出す関数。 colSums は行列の列ごとの和、rowSumsは行列の行ごとに和を取る関数がある。これを使うと Rではベクトルの計算は成分ごとに行ってくれるのでつぎのように計算できる。実際に試してみよ。

> tc <- test_a %>% select(true,cl_t) %>% table() 
> acculacy <- sum( diag(tc) ) / sum(tc)
> precision <- diag(tc) / colSums(tc)
> recall <- diag(tc) / rowSums(tc)
> f_measure <- 2 * precision * recall / (precision + recall)
> acculacy

[1] 0.9482

> precision

        A         B         C         D 
0.9545089 0.9249901 0.9422240 0.9719055

> recall

     A      B      C      D 
0.9484 0.9372 0.9524 0.9548

> f_measure

        A         B         C         D 
0.9514446 0.9310550 0.9472847 0.9632768

Table 15.1: 5点の座標
点	\((x,y)\)
C1	\((1,1)\)
C2	\((2,1)\)
C3	\((1,3)\)
C4	\((4,5)\)
C5	\((5,5)\)
C6	\((5,3)\)