7 決定木
決定木とはルールを木の構造で表すものである。まず、データの持つ特徴を表現する方法がなぜ木という形になるのかについて説明し、続いてデータからこうした木構造を導く方法について説明する。
キーワード
グラフ、木、分類木、回帰木、ジニ係数
7.1 木構造とデータの分割
相手に0から9までの数のうち,どれか1つを決めてもらい,いくつか質問をしていきながらその数を当てるというゲームを考えてみよう。 ヒントには「はい」か「いいえ」で答えてもらうことを考える。 最初に「5以上ですか?」と聞く。すると「はい」という答えなら 候補が 5から 9までの半分に減る。「1以上ですか?」と聞いたら運よく「いいえ」と答えてもらえればよいが,「はい」という答えのときに 候補がしぼれなくなってしまう。「5」の次の質問は「7以上ですか?」と聞く。こういって候補の中央の値以上かそれより小さいかという やり取りを繰り返していけば,多くとも4回の質問でどれかに辿りつくことになる。他にも,住んでいる都道府県をあてる場合には、「首都圏かそうでないか?」「周りに海があるかどうか?」などの条件によって 住んでいる県を分類していけば,いくつかの質問で相手の住む県を当てることができるかもしれない。 こうした例はデータの集合をある条件をもとに分割していったものである。 この例のように、考えている範囲をどんどんと狭めていこう。こうした作業を図で表すと、(1) のように 描くことができるだろう。

図において、で表された各点のことをノード(node)、また線のことをエッジ(edge)または枝という。 このように、ノードとエッジから作られる図形のことをグラフ(graph)という。 グラフは様々なノードがどのようにつながっているのかというネットワークの特徴を示そうとするものであり、 エッジの長さなどを変えることによって、同一のグラフであっても見た目が異なることがある。
また、このグラフの構造に着目すると、どのノードから出発しても、別の枝を通ってもとのノードに戻ってくるような 環状の道は存在しない。このようなグラフのことを特に木(tree)という。
木構造の頂点にあるものを根といい、枝分かれのもとを親ノード、先を子ノードという。根のある木を特に 根付き木という。根のノードが子ノードになることはないので、根ノードは親ノードを持たない。 一方、親ノードから分岐していき末端にあるものには子ノードがない。このように親ノードになっていないノードのことを 葉(leaf) という。 そして、子ノードの要素が1つか2つしかない木のことをニ分木という。 決定木の分析とは、データをもとにこのような木を作成することである。
例として(Figure 7.2)について考えてみよう。様々な特性の持つデータの集まりがあるとしよう。それをその特徴によって、図のように3本の線で分割した状況を考えてみよう。
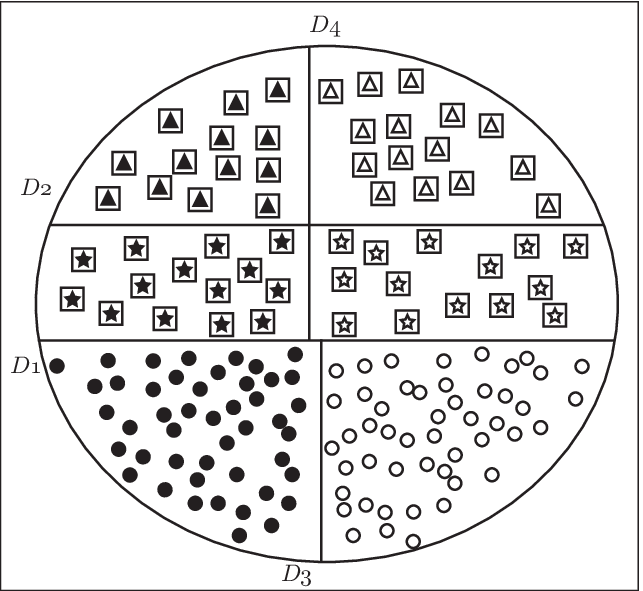
- の木構造はこれを D1、D2、D3、D4の順に分割したものである。 他にも D3、D4 をあわせた条件で分割し、次に、D1、D2 の順で分割すれば、異なった構造を持つ木ができることになる。 このような分割を人が判断する場合には、それぞれの分割について 「四角(□)に囲まれているか図形かどうか」、「黒塗りかどうか」といった条件を 考えることができるが、機械的にこうした木を作成するためには、分岐の条件についても考えなければならない。今回はデータの各成分の値に従って分類することを考える。
7.2 不純度とジニ係数
木構造を作るためには、何らかの基準でグループを分け、 そのそれぞれに対し、またさらにグループに分けてという作業を繰り返す。 では、どのようにしてグループに分けていけばよいだろうか。この問題を考えるために、次の例をもとに問題を定式化してみよう。例として、放送大学のように幅広い年齢層が受講するような、ある科目を考え、その科目の試験を受験した10人の試験結果が (Table 7.1) のようになったとしよう。 こうした変数のうち、分析対象にしたい変数については最初から決められていることが多い。 例えば先程の(Table 7.1) であれば、どういった人が70点以上なのかどうかを 調べたいと考えるだろう。このデータの変数は、それぞれ「ある値以上かどうか」といった具合に数種類(今は 2種類)のどれかの値しかとらないカテゴリー変数になっている。 目的変数がカテゴリー変数であるような決定木のことを分類木、目的変数が連続変数であるような 決定木を回帰木ともいう。
| 学生番号 | 年齢 | 性別 | 点数 |
|---|---|---|---|
| 1 | 40歳未満 | 男性 | 70点以上 |
| 2 | 40歳未満 | 女性 | 70点以上 |
| 3 | 40歳未満 | 男性 | 70点以上 |
| 4 | 40歳未満 | 男性 | 70点以上 |
| 5 | 40歳以上 | 男性 | 70点以上 |
| 6 | 40歳未満 | 男性 | 70点未満 |
| 7 | 40歳以上 | 女性 | 70点未満 |
| 8 | 40歳以上 | 女性 | 70点未満 |
| 9 | 40歳以上 | 男性 | 70点未満 |
| 10 | 40歳以上 | 女性 | 70点未満 |
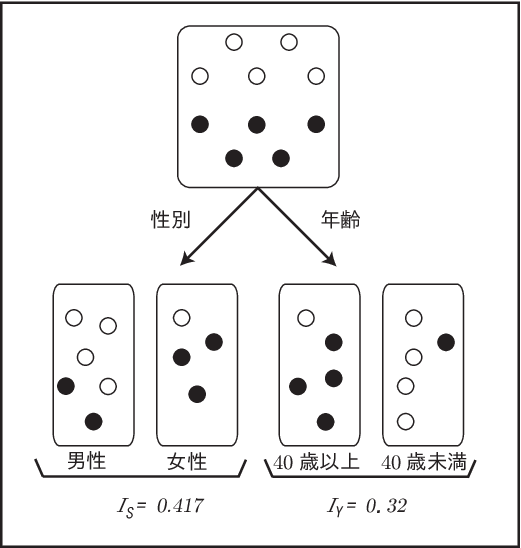
では、このデータを分割することを考えよう。 ここでは、1984年にブライマン(L.Breiman)らによって 提案されたCARTという計算手順(アルゴリズム)に基づいて 説明を行う。今、70点以上か未満かによって、データは 2つのクラスに分かれる。 そこで、「70点以上になる」 ということを A というクラスに属すると考え、「70点未満になる」ということを クラス B に属するとする。 今、Aに属する要素を ◯、Bに属する要素を ●であるとすると、 (Table 7.1) は(Figure 7.3) のように書くことができる。 では、分割として望ましいのはどちらであろうか。 データを分割する場合には、どういう場合に70点以上で、どういう場合に70点未満なのかということを知りたいので、 ◯ と ● が 混ざっている状態より、◯ と ● がうまく分離してくれるような条件で 分類する方が望ましいと考えることができる。 このように決定木ではデータの中の混ざり具合を表す 不純度を求める。 不順度について、 ジニ係数(Gini係数) という指標を考えよう。
ジニ係数はジニ(C. Gini) が1936年に考案した指数で、データからランダムに2つの要素を抜き出したときに、 その2つのデータがそれぞれ別のクラスに属する確率である。ここで、クラス\(A\)に属する確率を\(p_A\)、 クラス\(B\) に属する確率を\(p_B(=1-p_A)\)とすると、ジニ係数\(I\)は、
\[\begin{eqnarray} I &=& 1-p_A^2-p_B^2 =1-p_A^2-(1-p_A)^2=2p_A(1-p_A) \end{eqnarray}\]と表すことができる。 1つのデータを取り出し、もとに戻してからもう1度取り出したときに、どちらも \(A\) の属する確率は \(p_A^2\)、ともに \(B\) である確率は\(p_B^2\) であるから、全体からこれらの場合を取り除いた値は、 取り出したデータがそれぞれ別のクラスである 確率を表す。 一般にクラスが \(n\) 個ある場合には、
\[\begin{eqnarray} I &=& 1-p_1^2-p_2^2-\cdots-p_n^2 =1-\sum_{i=1}^{n}p_i^2 \end{eqnarray}\]と計算できる。 (Figure 7.3) をもとに計算してみよう。まず、分割する前のジニ係数\(I_P\)は、
\[\begin{eqnarray} \nonumber I_P &=& 1-\left(\left(\frac{5}{10}\right) ^2+\left(\frac{5}{10}\right) ^2 \right) \\ &=& 1-\frac{1}{2}=0.5 \end{eqnarray}\]である。性別で分類した場合と年齢で分類した場合のジニ係数を それぞれ、\(I_S\)、\(I_Y\)とすると、
\[\begin{eqnarray} \nonumber I_S(\mbox{男性}) &=& 1-\left(\left(\frac{4}{6}\right)^2+\left(\frac{2}{6}\right)^2 \right) =\frac{4}{9}=0.4444\cdots\\ \nonumber I_S(\mbox{女性}) &=& 1-\left(\left(\frac{1}{4}\right)^2+\left(\frac{3}{4}\right)^2 \right) =\frac{3}{8}=0.375 \end{eqnarray}\]である。 このジニ係数をそれぞれの個数の割合を掛けることで平均のジニ係数を求めると
\[\begin{eqnarray} \nonumber I_S&=&\frac{6}{10}\times\frac{4}{9}+\frac{4}{10}\times\frac{3}{8}=\frac{5}{12}=0.4166\cdots \end{eqnarray}\]となる。一方、
\[\begin{eqnarray} \nonumber I_Y(\mbox{40歳以上}) &=& 1-\left(\left(\frac{1}{5}\right)^2+\left(\frac{4}{5}\right) ^2 \right)=\frac{8}{25}=0.32 \\ I_Y(\mbox{40歳未満}) &=& 1-\left(\left(\frac{4}{5}\right)^2+\left(\frac{1}{5}\right) ^2 \right) =\frac{8}{25}=0.32 \end{eqnarray}\]なので、平均ジニ係数を求めると、
\[\begin{eqnarray} \nonumber I_Y&=&\frac{5}{10}\times\frac{8}{25}+\frac{5}{10}\times\frac{8}{25}=\frac{8}{25}=0.32 \end{eqnarray}\]となる。見比べてみると、不純度が高いほどジニ係数としては大きくなり、 逆に不純度が低いほどジニ係数が小さくなっていることがわかる。 分割する前と比較すると、
\[\begin{eqnarray} \nonumber \Delta I_{PS} &=& I_P-I_S =0.5-0.417=0.083 \\ \nonumber \Delta I_{PY} &=& I_P-I_Y =0.5-0.32=0.18 \end{eqnarray}\]となって、どちらも分割する前よりはデータの不純度は減っているが、 今回は年齢で分割する方が、性別で分割するよりも不純度が小さくなっている。 このように、決定木は、ジニ係数の差が最大となるような分岐を見つけ出し、そのそれぞれについても、 それ以上ジニ係数が小さくなることがないというところまで、分岐の作業を繰り返していく。
7.3 Rによるシミュレーション
Rでは決定木の分析を行うrpartというパッケージを用いる。 追加でインストールする必要があるので、 データとしては、架空の成績データを 利用することにする1。 これは次に示すような学生の試験結果を表すデータで、 表7-1 の例に加えて、試験を受けた回数を付け加えた100人分の 成績を表している。ここで、New とは1回目の受験を、Retryは再試験を意味している。 このデータを用い、どういったタイプの人が「70点以上」の成績を取るのかどうかということを分析する。
> s1 <- read_csv("data/rpart.csv")Rows: 100 Columns: 5
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (4): age, gender, trial, score
dbl (1): number
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.> s1 %>% head()# A tibble: 6 × 5
number age gender trial score
<dbl> <chr> <chr> <chr> <chr>
1 1 Under40 Man New Under70
2 2 Under40 Woman New Under70
3 3 Over40 Woman Retry Under70
4 4 Over40 Man New Over70
5 5 Over40 Woman New Over70
6 6 Under40 Man New Over70 次にlibrary(rpart)でライブラリの読み込みを行う。 今回は、どういったタイプの人が「70点以上」の成績を取るのかということを調べたいので、 4つの成分のうち、scoreが目的変数であり、他の変数が説明変数ということになる。 rpartでは、回帰分析のときに用いたlmと同様に目的変数~説明変数と指定する。 複数ある場合には +でつなぐ。score以外のすべてという場合には、ピリオド(.)のみ とすることができる。最後に、分類木であることを示すために method="class"と指定する。解析が終わったら結果を見てみよう。s2と打つと次のように結果が表示される。
> library(rpart)
> s2 <- rpart(score ~age+gender+trial,data=s1,method="class")
> s2n= 100
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 100 48 Under70 (0.4800000 0.5200000)
2) trial=New 70 29 Over70 (0.5857143 0.4142857)
4) age=Under40 34 6 Over70 (0.8235294 0.1764706) *
5) age=Over40 36 13 Under70 (0.3611111 0.6388889)
10) gender=Man 15 7 Over70 (0.5333333 0.4666667) *
11) gender=Woman 21 5 Under70 (0.2380952 0.7619048) *
3) trial=Retry 30 7 Under70 (0.2333333 0.7666667) *このように、受験回数によって分岐があり、 受験回数がNewであるグループはさらに年齢によって分岐があり、40歳以上であるグループはさらに性別によってさらに分岐が起こっている。 rpart.plot というパッケージをインストールし、そのパッケージにある rpart.plot という関数を用いるとつぎのような樹形図を作成してくれる。
# label: rpart.plot
# prompt: TRUE
library(rpart.plot)
rpart.plot(s2,box.palette = "Greys")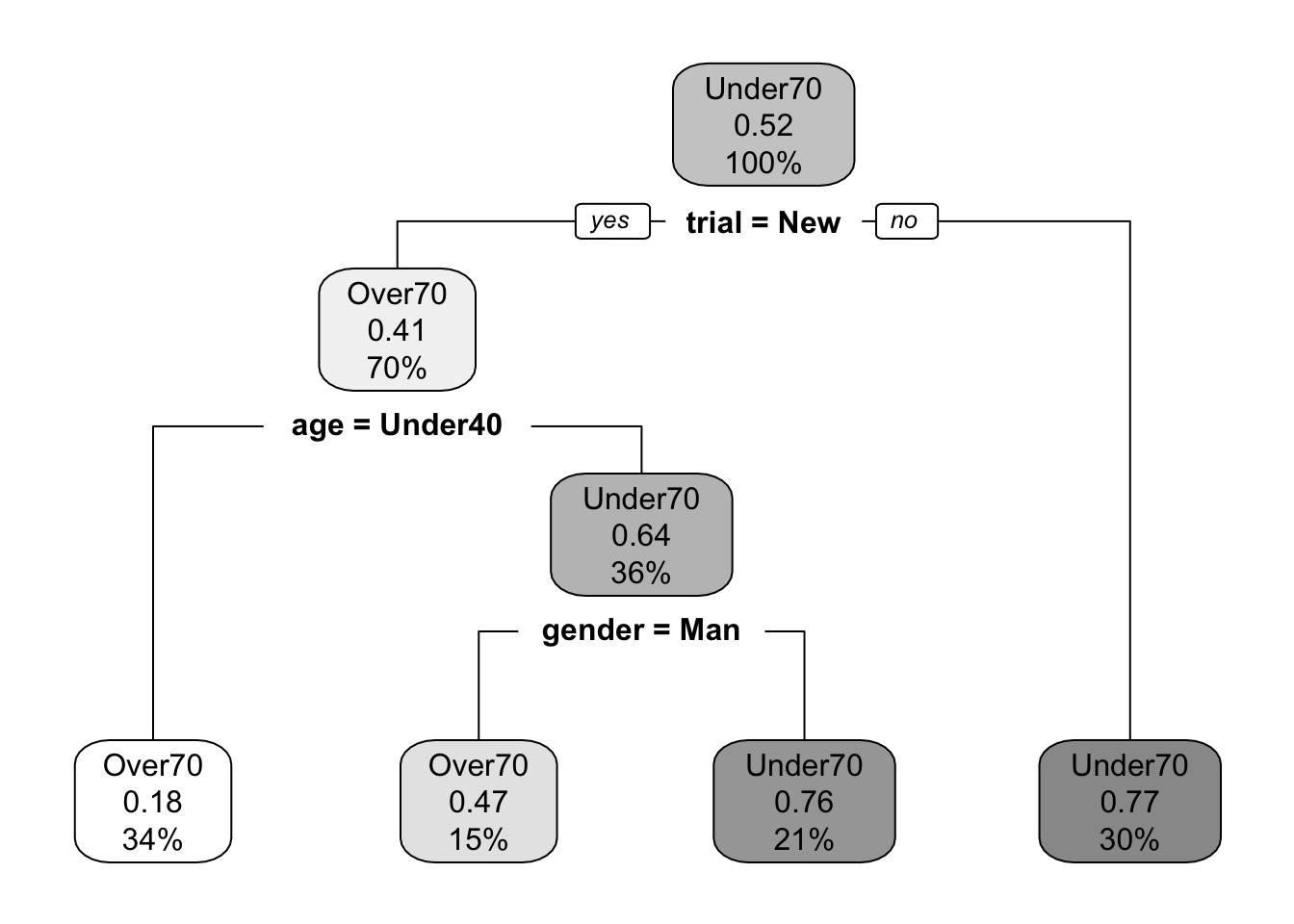
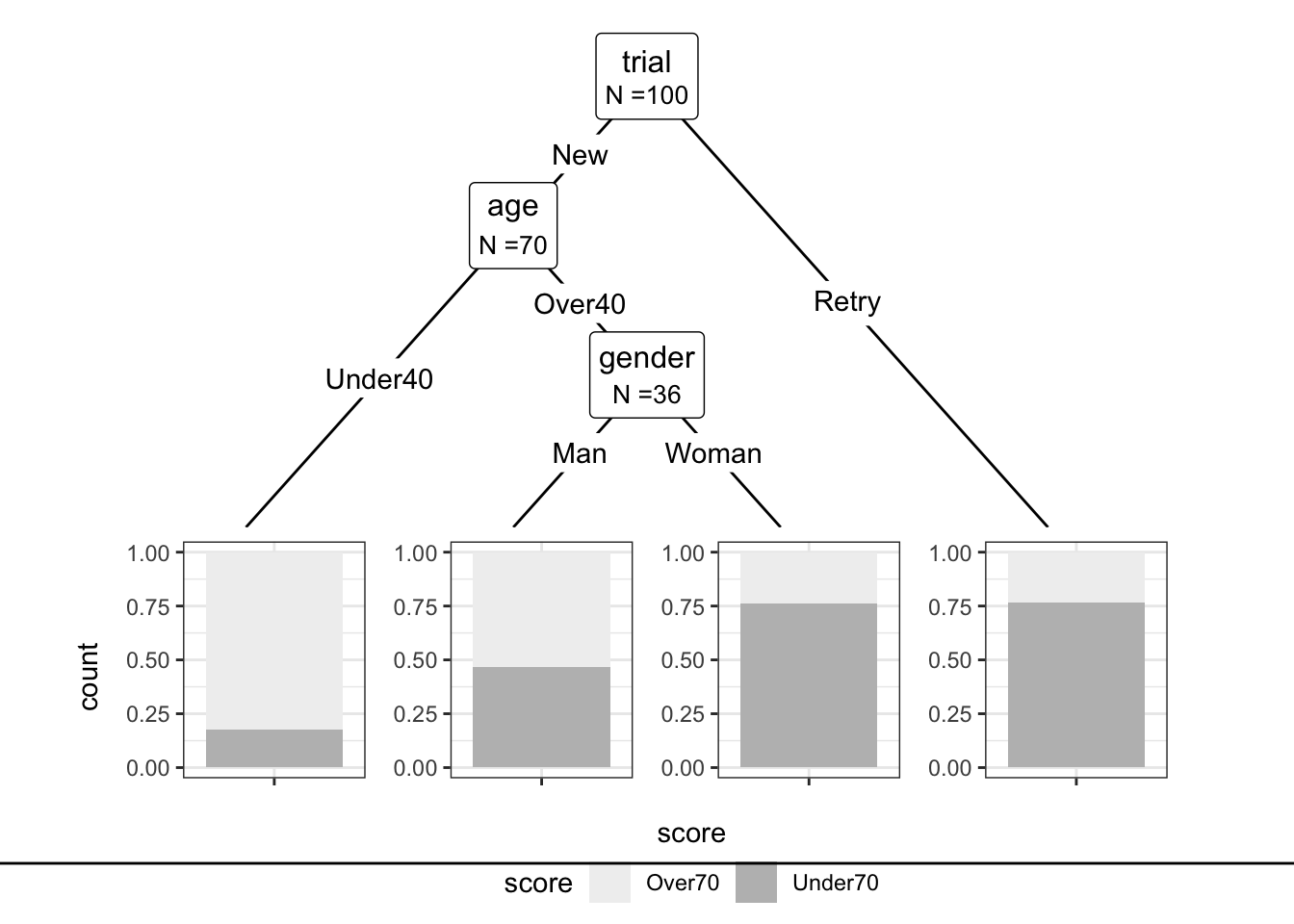
これを見ると、再試験を受けている人は70点未満であることが多い。 また、1回目の受験の中でも40歳未満の場合に70点以上の割合が高く、逆に40歳以上の女性が70点以下であることが多いというように 分類されていることが見て取れる。 ggplot 系のグラフとしては ggparty というパッケージがある。ggplotの代わりに ggparty でデータを指定する。 geom_edgeが枝の描画、geom_nodeが 点を表示する。idsはinnerが枝分かれの点、 terminal が終点を意味している。
> library(ggparty)
> s3 <- as.party(s2)
> ggparty(s3) +
+ geom_edge() +
+ geom_edge_label() +
+ geom_node_label(
+ line_list = list(
+ aes(label = splitvar),
+ aes(label = paste0("N =", nodesize) ) ),
+ line_gpar =list(
+ list(size=12,parse=T),
+ list(size=10,parse=F) ),
+ ids = "inner") +
+ geom_node_plot(
+ gglist = list(geom_bar(aes(x="", fill = score),
+ position = "fill"),
+ labs(x="score"),theme_bw(),
+ scale_fill_brewer(palette="Greys") ),
+ scales = "fixed",
+ id = "terminal",
+ shared_axis_labels = TRUE,
+ legend_separator = TRUE,
+ )
7.4 まとめと展望
ここでは、決定木について、特に分類木について説明した。 決定木は不純度を表す指標をもとにデータを分割し、 その不純度が最も小さくなるように分岐を決定した。 今回はジニ係数を用いたが、ジニ係数の代わりに 情報理論の情報量という概念が用いられることがある。 情報量は \(\log_2(p_i)\)で表され、その情報量の平均のことをエントロピーという。 エントロピーは、 \[ I=-\sum_{i=1}^{n}p_i\log_2(p_i) \] と計算される。ここで、\(0\log_2(0)=0\)とする。 エントロピーは情報の不確実さを表したものである。ある確率分布が与えられるとそのエントロピーを計算することができる。たとえば、結果が \(n\) 通りある場合の エントロピーは、どれも等確率 \(p_i=\frac{1}{n}\) で起こるときに最大になる。決定木の場合には、分割することによって、このような不確実性を減らすようにしたいので、 分割の前後でのエントロピーの差とは分割前の情報量の平均から分割後の情報量の平均を引いた値が 最大になるように分割する。 この差のことを情報利得という。 要素が2つの場合のジニ係数とエントロピーのグラフを (Figure 7.4)に示す。
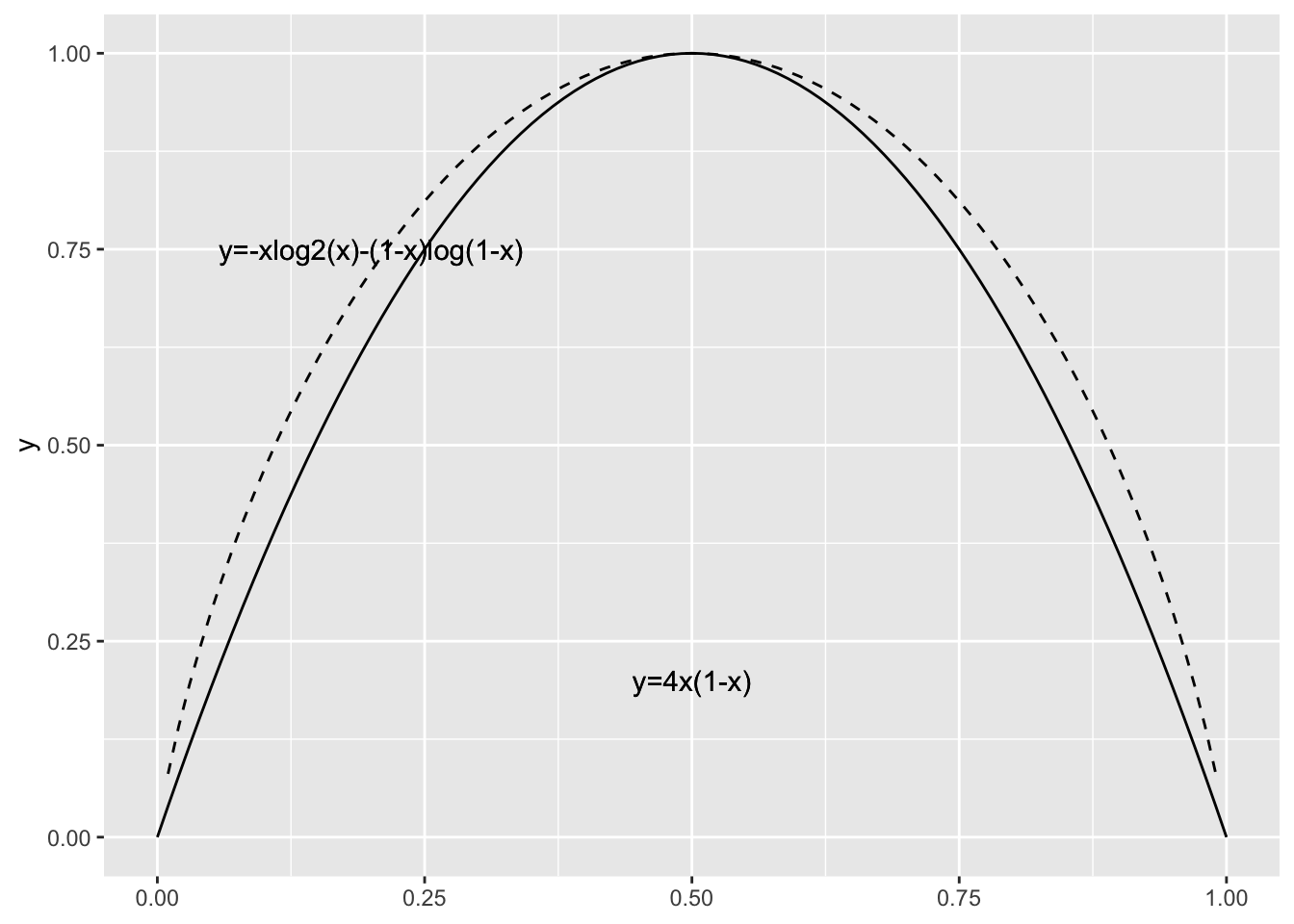
決定木では扱うデータの説明変数の量が多くなると、 それに合わせて深く広く枝分かれをするということが起きてしまう。 このような場合の細かな枝分かれとは必ずしも本質的な違いとは限らず、収集したデータのみが 持つ微妙な違いに応じた分岐でしかないということも起こる。このような現象を過学習という。 こうしたことが起きないためには、細かく分岐した枝をある判断基準のもとで切るということを行う。 これを枝刈りまたは剪定(pruning)という。
また、単独で精度が低い場合であっても複数の機械を用いることで精度が向上することがある。それぞれ並列に学習させた学習器を複数用いて多数決や平均によって最終的な分類予測を行うものをアンサンブル学習という。決定木を複数組み合わせて分類予測をするものを ランダムフォレストという。 R ではランダムフォレストを行うパッケージに randomForest がある。
参考文献
[1]. Bradley Efron,Trevor Hastie(著), 井手剛,藤澤洋徳(訳), “大規模計算時代の統計推論 : 原理と発展”, 共立出版,2020,https://hastie.su.domains/CASI/ }
[2]. Trevor Hastie,Robert Tibshirani,Jerome Friedman(著), 杉山将,井手剛,神嶌敏弘,栗田多喜夫,前田英作(訳), “統計的学習の基礎 : データマイニング・推論・予測”, 共立出版,2014,https://hastie.su.domains/ElemStatLearn/
[3]. 金明哲,“R によるデータサイエンス(第2版)”,森北出版,2017
演習
誤っている部分を直せ
木とはループのないグラフのことである。
目的変数がカテゴリー変数の決定木を特に分類木という。
データを分割するときは不純度が小さくなるように分類する。
ジニ係数はデータのばらつきを表し、値が大きいほどばらついていることを意味している。
決定木では細かな枝分かれが必ずしも本質的な違いに対応しているわけではなく、枝分かれが多いほどよいとは限らない。
7.5 補則
. 今回は説明変数がすべてカテゴリー変数の場合を説明したが、説明変数が連続変数の場合、ある値で分割する。 また、目的変数も量的変数の場合はグループ分けした 回帰木では、目的変数を \(y\) 、説明変数の1つを \(x\) とし たとき、\(x\geqq s\) のグループを\(R_1\)、\(x<s\) のグループを\(R_2\) とし、各グループの\(y\)の平均を \(\bar{y}_{R1}\)、\(\bar{y}_{R2}\)とすると、 \[ \min \left\{ \sum_{x\in R_1} ( y - \bar{y}_{R1} )^2 + \sum_{x\in R_2} ( y - \bar{y}_{R2} )^2 \right\} \tag{7.1}\]
を計算する。
> set.seed(0)
> N_train <- 20
> sigma <- 0.1
> train_x <- runif(N_train)
> train_y <- sin(2*pi* train_x) + rnorm(N_train,0,sigma)
> a <-rpart(train_y~train_x)
> rpart.plot(a,box.palette = "Greys")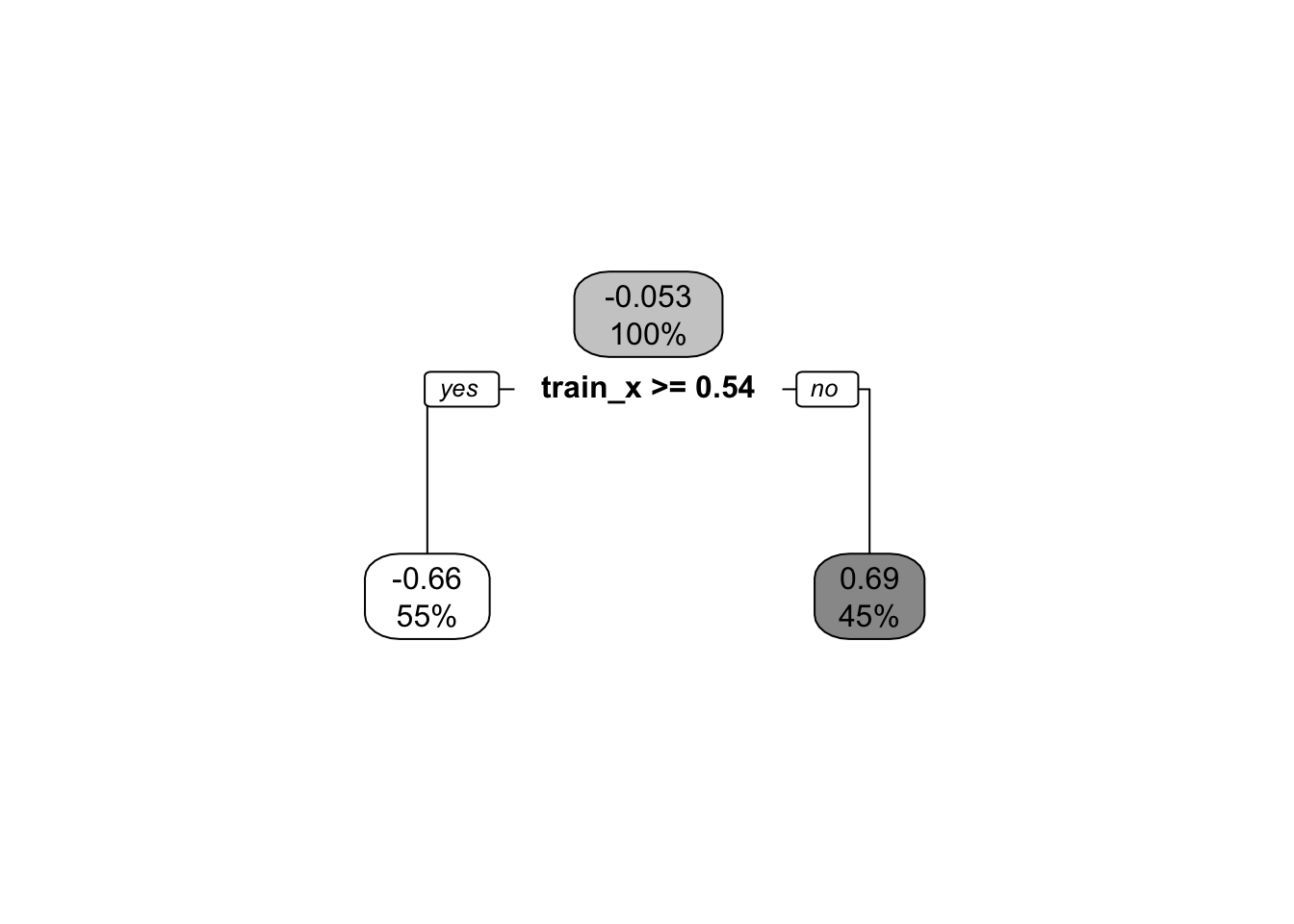
上の例では、全体の\(y\) の平均が -0.0534543 で \(x\) が 0.5352763 かどうかで分割し、 それぞれの\(y\) の値を -0.6580945 -0.6580945 とするルールを抽出している。
> an= 20
node), split, n, deviance, yval
* denotes terminal node
1) root 20 10.2940700 -0.0534543
2) train_x>=0.5352763 11 0.6721920 -0.6580945 *
3) train_x< 0.5352763 9 0.6852348 0.6855504 *MSE はグループ内の平均2乗和を表している。 式(7.5) において、全体の平均を \(\bar(y)\) とすると
\[\begin{eqnarray} \nonumber \sum_{all}(y_i-\bar{y})^2 &=& \sum_{x \in R_1 }(y_i-\bar{y}_{R1} )^2 + \sum_{x \in R_2 }(y_i-\bar{y}_{R2} )^2 +\\ \nonumber & & \left( n_{R1}(\bar{y}_{R1}-\bar{y})^2 + n_{R2}(\bar{y}_{R2}-\bar{y})^2 \right ) \end{eqnarray}\]が成り立つ。前半の二項は同じグループ内の ばらつき、後半の二項は群ごとのばらつきを 表している。同じグループ内のばらつきが小さくする ことが不純度を小さくすることに対応している。
Over70と Under70では厳密には70点が含まれないが、 ここでは分かりやすさを優先して Over70とUnder70 と記す。↩︎