9 回帰分析（２）

説明変数が複数ある場合の重回帰分析について説明し、説明変数同士の関係を見る方法として偏相関係数について説明する。重回帰分析の例として非線形関数の多項式近似を行う方法について説明する。最後に回帰係数の検定について述べ、Rでシミュレーションを行う。

キーワード

偏相関係数、多項式近似、自由度、信頼区間

9.1 偏相関係数

回帰分析では説明変数をどのように選ぶかが問題となる。このときある変数\(X_i\)の偏回帰係数が大きい場合でも、他の変数の影響を受けて大きくなることもあり、直接の影響かどうか判断することができない。そこで、説明変数のある変数が目的変数との関係を見る上で 偏相関係数が用いられる。たとえば変数\(X_1\)から\(X_{r-1}\)までを固定した \(X_r\)と\(Y\)との偏相関係数は

\[\begin{eqnarray} \hat{x}_r &=& \hat{b}_0+\hat{b}_1 X_1+\hat{b}_2 X_2 + \cdots \hat{b}_{r-1}X_{r-1}+E_r \\ \hat{y} &=& \hat{c}_0+\hat{c}_1 x_1+\hat{c}_2 x_2 + \cdots \hat{c}_{r-1}x_{r-1}+E_y \end{eqnarray} \]

として表した\(E_r\)と\(E_y\)との相関係数として計算される。例として変数が3個の場合に\(X_1\)を固定した場合、 \[ E_{2}= -\frac{s_{12}}{s_{11}}(X_1 - \mu_{1}) +(X_2-\mu_{2})\\ E_{y}= -\frac{s_{1y}}{s_{11}}(X_1 - \mu_{1}) +(Y-\mu_{Y}) \] の相関係数として

\[\begin{equation} r_{2y\cdot 1} = \frac{s_{11}s_{2Y}-s_{12}s_{1y}}{\sqrt{s_{11}s_{22}-s^{2}_{12}}\sqrt{s_{11}s_{YY}-s^{2}_{1Y}}} \\ \end{equation}\]

または

\[\begin{equation} r_{2y\cdot 1} = =\frac{r_{2y}-r_{12}r_{1y}}{\sqrt{1-r^{2}_{1y}}\sqrt{1-r^{2}_{12}}} \end{equation}\]

と計算される(右辺における \(r_{\cdot}\)はそれぞれの相関係数)。

9.2 重回帰分析による多項式近似

\(y=\sin(2\pi x)\) を多項式\(1,x,\cdots,x^{m-1}\) で近似することを考えてみよう。入力は0から1 の中で N_train個の一様乱数とする。観測される \(y\) には誤差が含まれているものとして、誤差が平均0、分散0.1 の正規乱数を付け加える。

> set.seed(0)
> N_train <- 20
> sigma <- 0.1
> train_x  <- runif(N_train)
> train_y <- sin(2*pi* train_x) + rnorm(N_train,0,sigma)

次に、ベクトルとして x を与えたときにそれぞれを\(1\) から\(m\)乗したものを行列として作成する関数 func_phi_poly を作る。関数は1行の場合には、{} で囲まずに書くことができる。 map は purrr というパッケージ（tidyverseに含まれている）にある繰り返しを行う関数。それについてはここでは説明を省略する。

> func_poly <- function(m,x) x^m
> func_phi_poly <- function(m,x_n){
+   phi <- vector("list",length=m)
+   phi <- map(1:m,func_poly,x=x_n)
+   phi <- matrix(unlist(phi),ncol=m)
+   colnames(phi) <- str_c("x",1:m)
+   phi <- as_tibble(phi)
+ }

例として m=4としよう。m の数は train_x を超えないようにする。以下の手続きをすることで、訓練用のtibbleができる。

> m <- 4
> df_train <- func_phi_poly(m,train_x)
> df_train <- df_train %>% mutate(y=train_y)
> head(df_train)

# A tibble: 6 × 5
     x1     x2      x3      x4      y
  <dbl>  <dbl>   <dbl>   <dbl>  <dbl>
1 0.897 0.804  0.721   0.647   -0.528
2 0.266 0.0705 0.0187  0.00497  0.915
3 0.372 0.138  0.0515  0.0192   0.605
4 0.573 0.328  0.188   0.108   -0.471
5 0.908 0.825  0.749   0.680   -0.575
6 0.202 0.0407 0.00820 0.00165  0.913

R の lm は切片が含まれている。もし切片を含めないのであれば lm(data=df_train,y ~ x1+x2+x3+x4-1 ) のように-1 とする。すべての列を用いて予測する場合には . で列名の指定を省略できる。

> lm_poly <- lm(data=df_train,　y ~ . )

結果を下に予測を行ってみよう。検証用データは等間隔に N_test個用意する。予測する場合には predict() という関数がある。係数を求めた lm_poly と入力 df_testを指定する。

> func_sin <- function(a,x) sin(a*x)
> N_test <- 200
> x_min <- 0
> x_max <- 1
> x_int <- (x_max - x_min ) / (N_test - 1)
> test_x  <- seq(x_min,x_max,x_int)
> df_test <- func_phi_poly(m,test_x)
> test_y <- predict(lm_poly,newdata = df_test)
> df_test %<>% mutate(y = test_y)

> ggplot(data.frame(x = c(0,1) ),aes(x=x) )+
+   geom_function(fun =func_sin,args=list(a=2*pi) )+
+   geom_point(data=df_train,aes(x=x1, y=y), col= "black")+
+   geom_line(data=df_test,aes(x=x1, y=y), linetype= "dotted")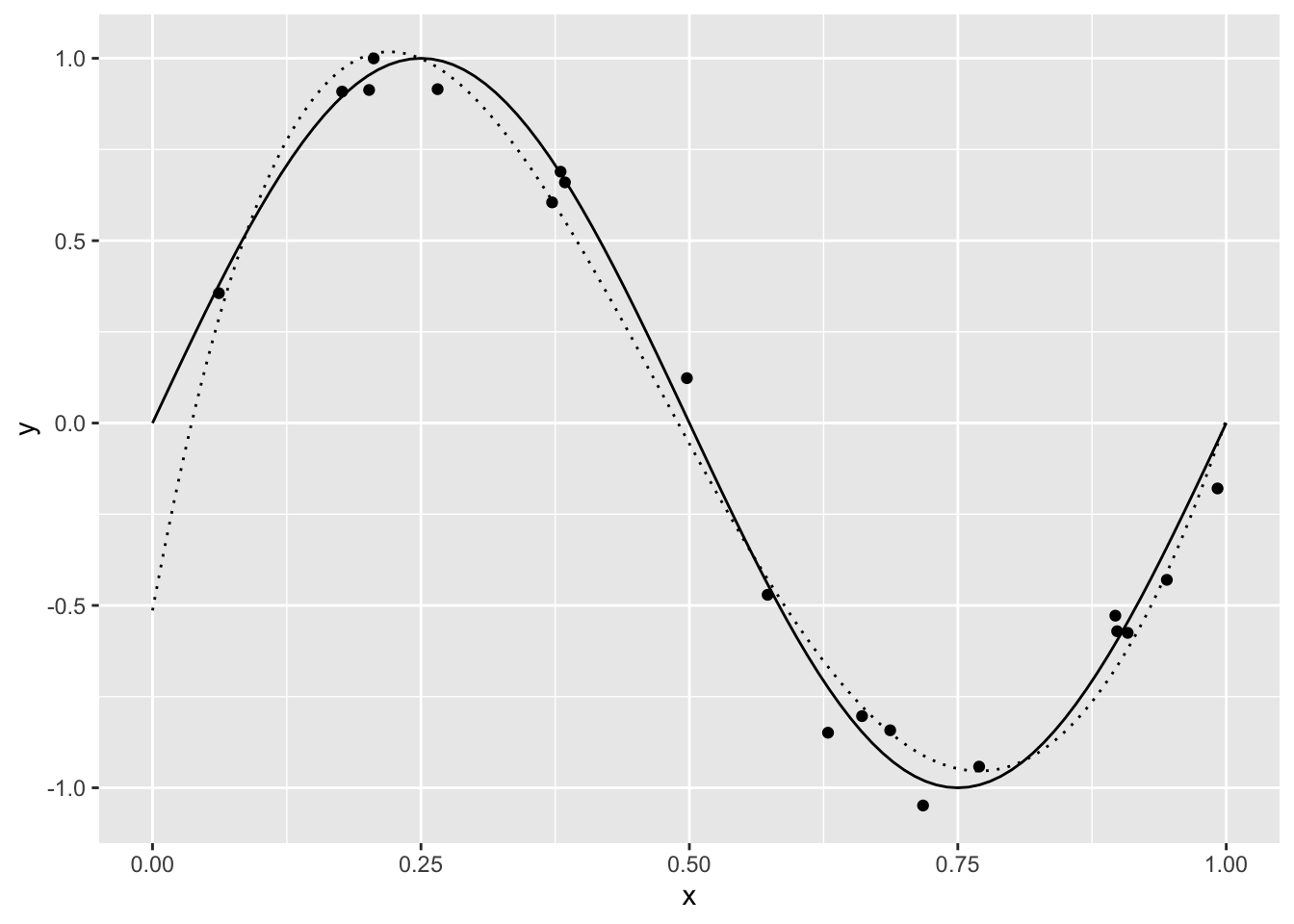

9.3 回帰係数の検定

前章で行った単回帰分析のシミュレーションをもう一度行ってみよう。今度は \(a=0\)、\(b=0\) として乱数を発生させて回帰係数を求める。その結果を見ると、例えば set seed(0) として行うと

              Estimate Std. Error    t value  Pr(>|t|)
(Intercept) -0.0791256  0.1324205 -0.5975329 0.5506968
x1           0.2090684  0.2298572  0.9095579 0.3639388

となる。この例では \(a=0.209\)、\(b=-0.079\) と推定された。summary() を見ると

> summary(w)


Call:
lm(formula = y1 ~ x1)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.91908 -0.69723 -0.03187  0.61162  2.57173 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.07913    0.13242  -0.598    0.551
x1           0.20907    0.22986   0.910    0.364

Residual standard error: 0.9749 on 248 degrees of freedom
Multiple R-squared:  0.003325,  Adjusted R-squared:  -0.0006941 
F-statistic: 0.8273 on 1 and 248 DF,  p-value: 0.3639

となっている。これについてもう少し詳しく見てみよう。確率変数 \(Y\) が　\(確率変数\) \(Y=aX+b+\epsilon\)　という関係があり、 \(\epsilon\) が正規分布に従うとき、先ほどの計算によって導かれた回帰係数の推定値\(\hat{a}\)、\(\hat{b}\)は平均\(a\)、平均\(b\) の正規分布に従う。しかし、\(\epsilon\) の標準偏差が事前にわかっているわけではない。そこで、

\[\begin{equation} \hat{\sigma}= \frac{S_R}{n-2} \end{equation}\]

をその標準偏差の推定値とするとき、 \(a\)、\(b\)の標準偏差は

\[\begin{equation} \hat{\sigma}_a = \frac{\hat{\sigma}}{S_{xx}} \\ \hat{\sigma}_b = \hat{\sigma} \sqrt{ \frac{1}{n} +\frac{\bar{x}^2}{S_{xx}} } \end{equation}\]

と推定される。したがって、

\[\begin{equation} T_a =\frac{\hat{a}-a}{\hat{\sigma_a}} \\ T_b =\frac{\hat{b}-b}{\hat{\sigma_b}} \end{equation}\]

は自由度 \(N-2\) のt分布の従う。先ほどのsummary()では \(a=0\) 、\(b=0\) を帰無仮説として \(t\) 検定を行った結果である。また、 \[ \sum_{p=1}^{N}({y}^{(p)}-\mu_y)^2 = \sum_{p=1}^{N}(y^{(p)}-\hat{y}^{(p)})^2 +\sum_{p=1}^{N}(\hat{y}^{(p)}-\mu_y)^2 \] について示した。左辺についてサンプルサイズ \(N\) のうち、平均を計算するのに1つの式を用いている。観測値のサンプルサイズから、推定に用いた式を除いた数を自由度という。推定した値を固定すると、\(N-1\)個の観測値が分かれば、平均から残りの値を定めることができる。右辺の第一項はN個のうち、回帰係数の推定に2個用いているので自由度は \(N-2\) である。残る第二項の自由度は \(1\) となる。これを \[ S_T = S_E+S_R \] とすると、この、\(S_E\)は自由度\(N-2\)のF分布、\(S_R\)は自由度\(1\)のカイ二乗分布に従い、この比 \[ F = \frac{S_R}{1} / \frac{S_E}{N-2} \] は自由度\((1,N-2)\)のF分布に従ううことが知られている。最後のメッセージでは\(a=0\) かつ\(b=0\) という帰無仮説の下で検定している。つまり、\(a=0\) であるという仮定を置いた場合に、この推定値の値を実現する確率（\(p\)値）を求めている。これが滅多に起こらない 0.05以下であれば * 、0.01以下であれば ** というように表記をしている。これについて、もう少し考えてみよう。\(a=0\)、\(b=0\) として乱数を発生させて、そこに正規乱数を加えて、観測データを作る。そのデータから\(a\)、\(b\)の値、およびt値、F値を計算する。このことを何度も繰り返し、それぞれヒストグラムを作ってみる。

> set.seed(5)
> true_a = 0
> true_b = 0
> samplesize <- 250
> trial = 1000
> x1 <- runif(samplesize)
> sim_Ta <- vector("numeric",length=trial)
> sim_Ta <- vector("numeric",length=trial)
> sim_Tb <- vector("numeric",length=trial)
> sim_F <- vector("numeric",length=trial)
> for(i in 1:trial){
+   x2 <- rnorm(samplesize,mean=0,sd=1.0)
+   y1 <- true_a*x1+ true_b + x2
+   w <- lm(y1~x1)
+   ahat <- w$coefficients[2]
+   bhat <- w$coefficients[1]
+   SX <- sum ( (x1-mean(x1))^2 )
+   SR <- sum ( ( w$fitted.values-mean(y1) ) ^2 )
+   ST <- sum ( w$residuals^2 )
+   MSR <- SR/1
+   MST <- ST/(samplesize-1-1)
+   sim_F[i] <- MSR/MST
+   sigmahat <- sqrt(ST/ ( samplesize- 2 ) )
+   sigma_a <- sigmahat/sqrt(SX)
+   sim_Ta[i] <- (ahat-true_a)  / sigma_a
+   sigma_b <- sigmahat*sqrt(1/samplesize + mean(x1)^2/SX )
+   sim_Tb[i] <- (bhat-true_b)  / sigma_b
+ }
> #| fig-cap: Ta のヒストグラム と t分布の比較 
> ggplot()+geom_histogram(aes(x=sim_Ta
+                             ,y=after_stat(density) ) ) +
+   geom_function(data=data.frame(x=c(-3,3) ),aes(x=x),
+                 fun=dt,args=c(df=(samplesize-2)))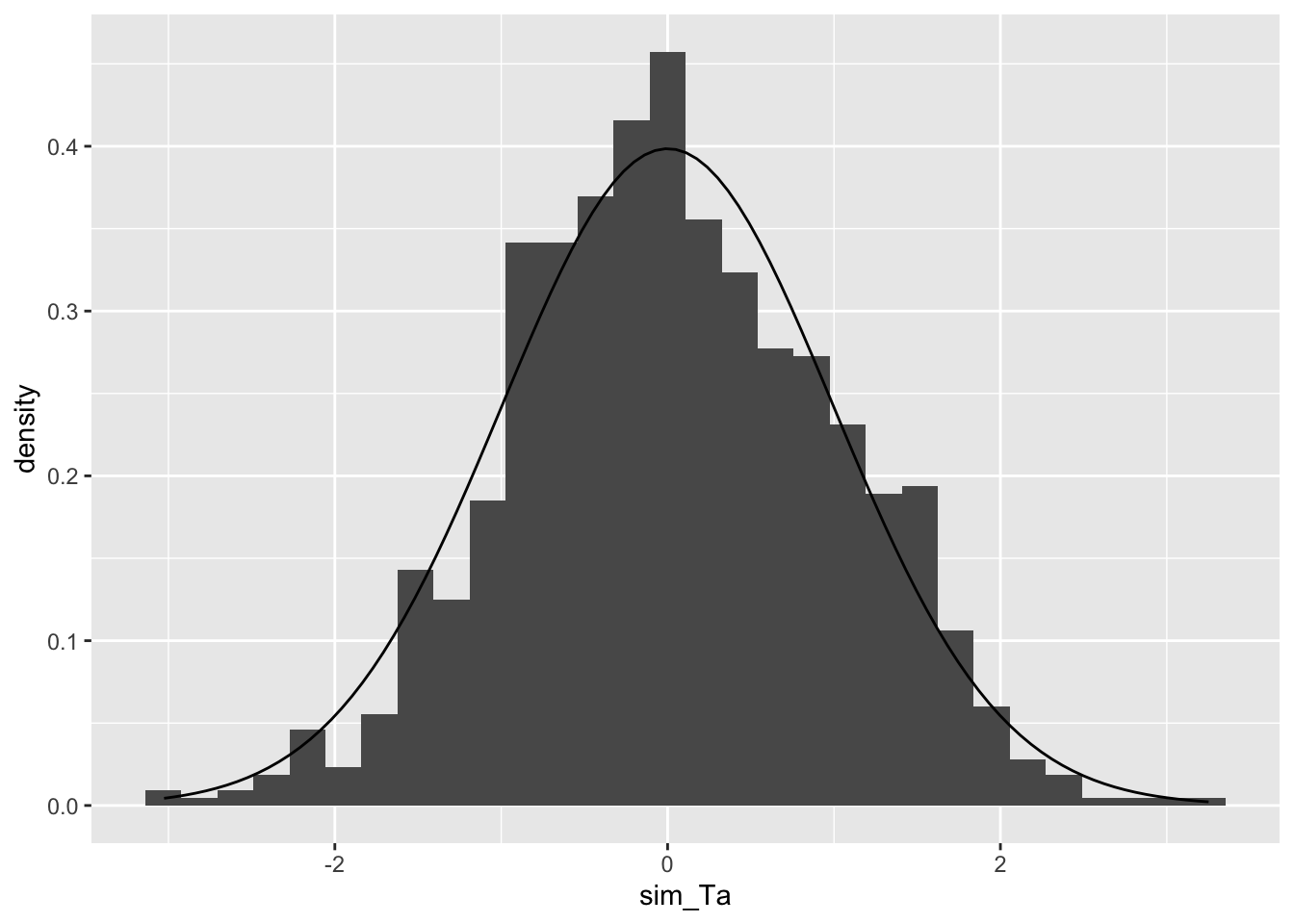

> #| fig-cap:　Tb のヒストグラム と t分布の比較 
> ggplot()+geom_histogram(aes(x=sim_Tb,y=after_stat(density) ) ) +
+   geom_function(data=data.frame(x=c(-3,3) ),aes(x=x),
+                 fun=dt,args=c(df=(samplesize-2)))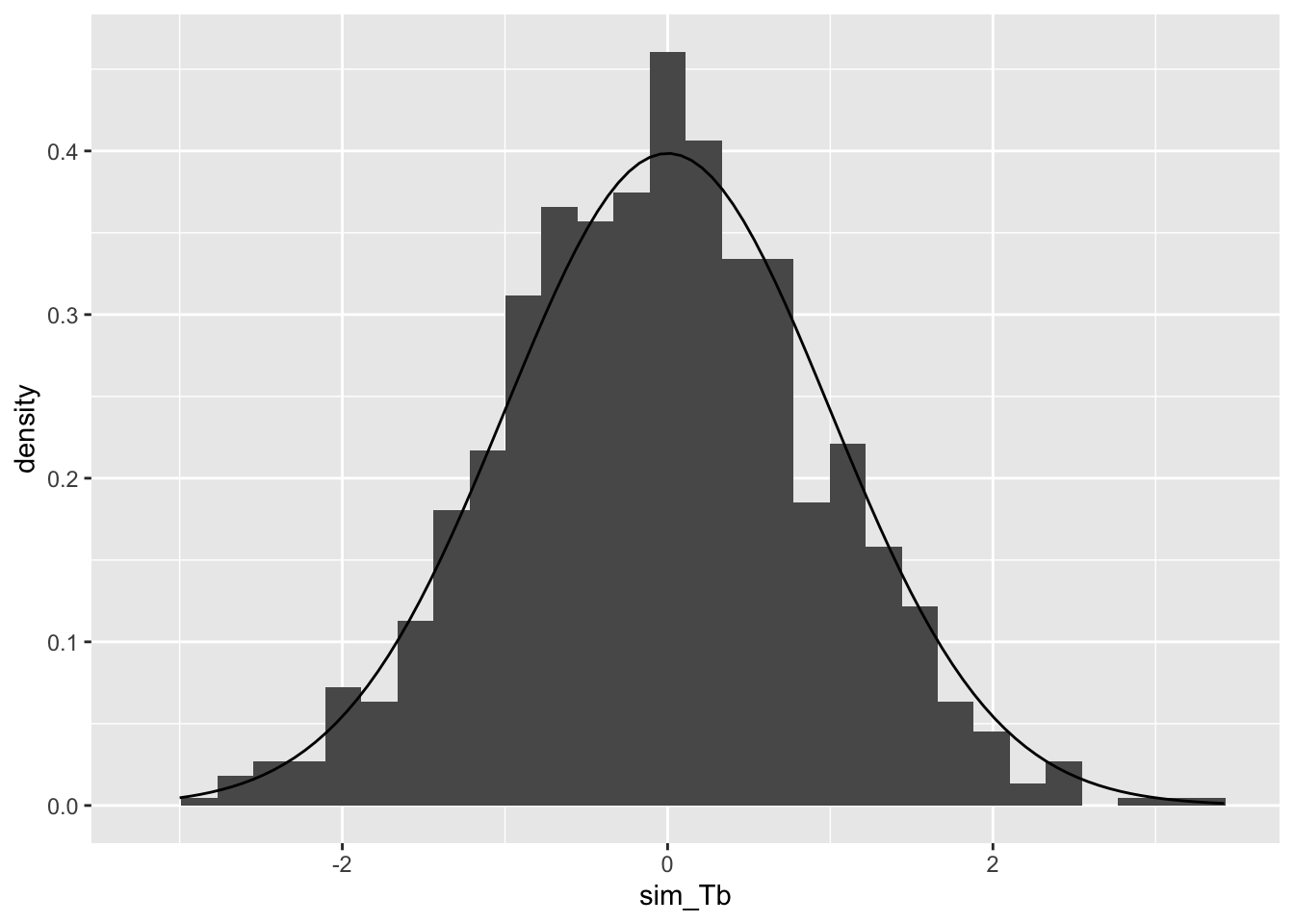

> #| fig-cap:　F のヒストグラムとF分布の比較 
> ggplot()+geom_histogram(aes(x=sim_F,y=after_stat(density)) )+
+   geom_function(data=data.frame(x=c(0,3) ),aes(x=x),
+                 fun=df,args=c(df1=1,df2=samplesize-2) )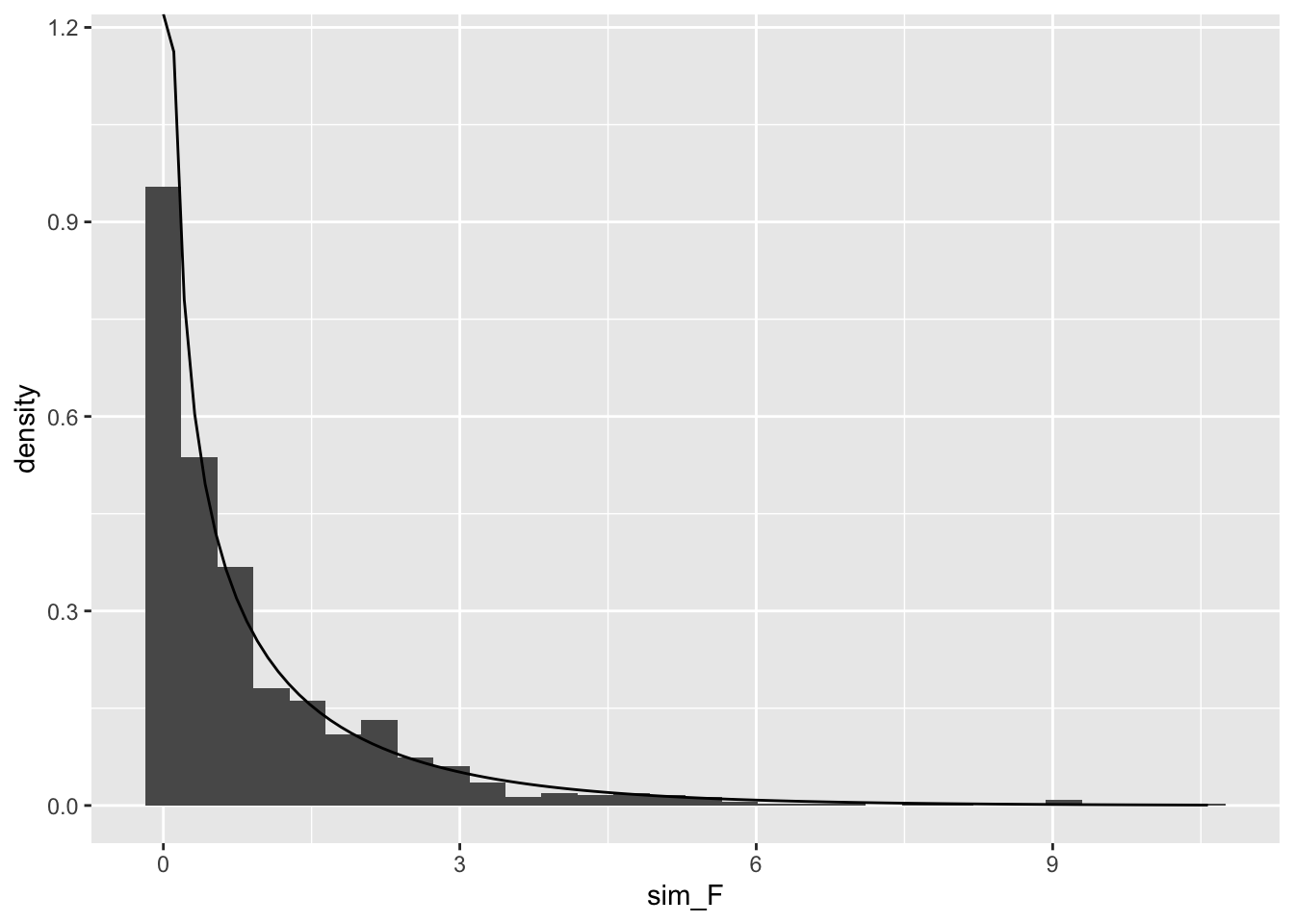

このグラフをみると、t分布やF分布にフィットしていることがわかる。t値は0を中心としており、0から離れているほど起こりにくい。そこで、t値が正の場合には 1 - pt()の値を 2倍し、負の場合にはpt()の値を2倍した値が Pr(>|t|) に表示されている。この例で

> sum( sim_Ta < qt(0.025,samplesize-2) )+ 
+   sum(sim_Ta > qt(0.975,samplesize-2))

[1] 39

> sum( sim_Tb < qt(0.025,samplesize-2) )+ 
+   sum(sim_Tb > qt(0.975,samplesize-2))

[1] 42

> sum( sim_F < qf(0.025,1,samplesize) )+ 
+   sum(sim_F > qf(0.975,1,samplesize-2))

[1] 49

とすると 5%の検定で外れた回数を数えることができる。

9.4 信頼区間の表示

前章で行ったシミュレーション結果をもう少し詳しく見てみよう。 predictでは信頼区間を計算することができる。

> set.seed(50)
> true_a <- 2
> true_b <-  3
> samplesize <- 100
> testsize <- 1000
> xint <- (1-0)/(testsize-1)
> x1 <- runif(samplesize)
> x2 <- rnorm(samplesize,mean=0,sd=1.0)
> y1 <- true_a*x1+ true_b + x2
> train <- tibble(y=y1,x=x1)
> w <- lm(y~x,data=train)
> test <- tibble(x = seq(0,1,xint) )
> y2 <- predict(w,newdata=test,interval="confidence") 
> head(y2,n=6L)

       fit      lwr      upr
1 2.746966 2.354650 3.139283
2 2.749096 2.357396 3.140796
3 2.751226 2.360142 3.142310
4 2.753356 2.362888 3.143825
5 2.755486 2.365633 3.145340
6 2.757616 2.368378 3.146855

となる。

ggplot では geom_smooth という関数があり、信頼区間を濃い色で表示し、predictによって求めた上限、加減を線で結んでいる。次のプログラムを実行してみよ。

> test <- cbind(test,y2)
> ggplot(data=train,aes(x=x,y=y))+geom_point( )+
+   geom_smooth(formula = y~x,method="lm")+
+   geom_line(data=test,aes(x=x,y=lwr),color="red")+
+   geom_line(data=test,aes(x=x,y=upr),color="red")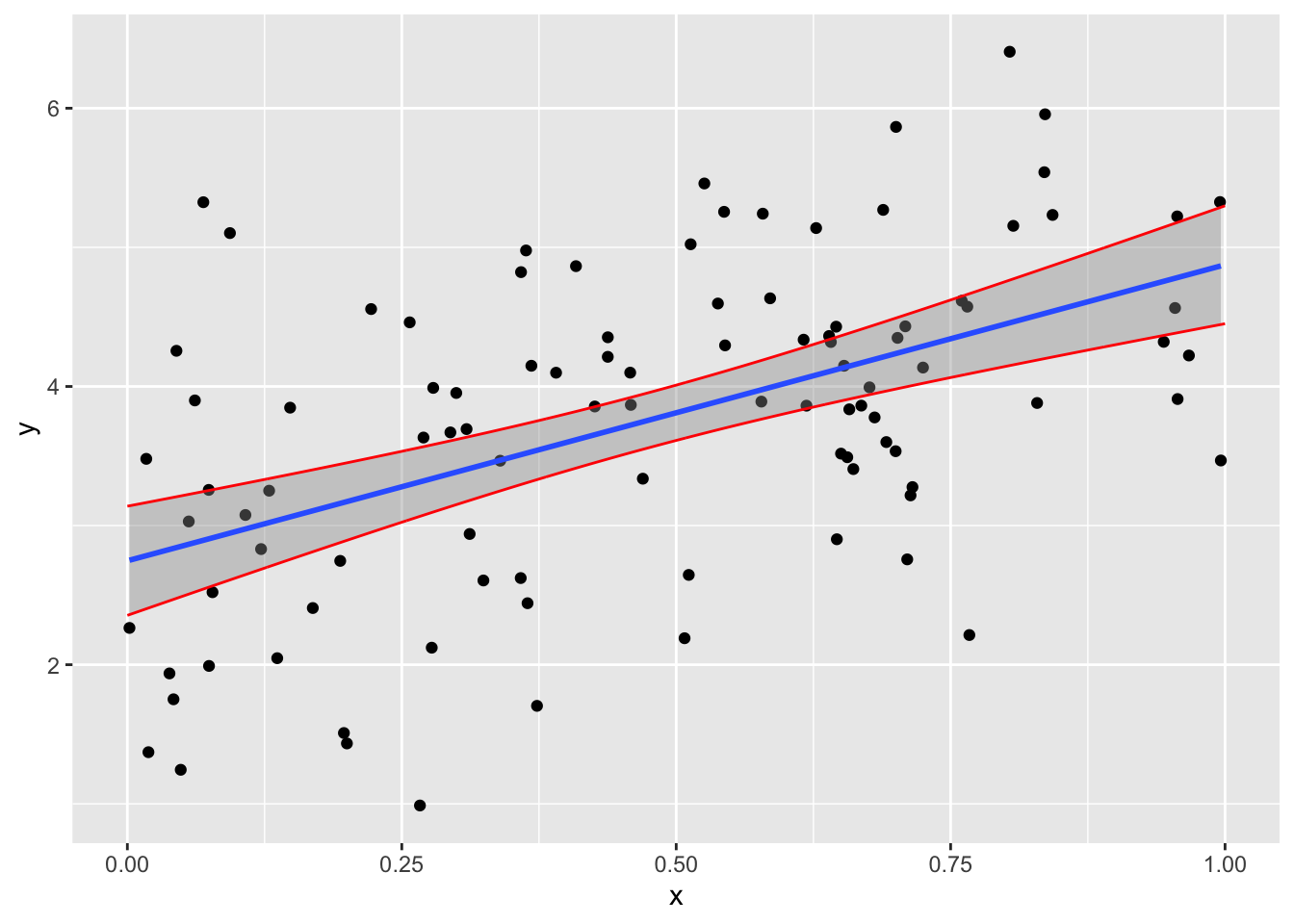

9.5 まとめと展望

説明変数の線形結合によって表すここでは線形回帰について述べた。 R を用いるとサンプルサイズの値を変えたり、与えるノイズと精度がどうなるのかといったことを調べることができる。後半では\(a=0\)、\(b=0\)、として観測データを作成し、分布を作成した。統計的仮説検定で低い \(p\)値が得られると仮説を棄却するが、低い \(p\)値は確率が低いということであり、全く起こらないということではない。今回の計算で分布が再現できたということは滅多に起きないことも低い確率で起こっていたということが確認できる。もちろん、こういうことができるのは、統計的な性質を満たすような乱数が用意されたシミュレーション環境だからこそできることで、現実の世界においては行えるわけではないが、それでも、手法の理解するという意味では非常に有効だと思うので色々と試してほしい。

実データにおいては、逆行列を持つ場合であっても行列式が正確に \(0\) になるわけではないが、とても小さいというような場合に、信頼性が低くなることがある。これを 多重共線性という。そして、説明変数を選ぶ段階で、ある程度それぞれの関係について知っておく必要がある。説明変数同士がどのような関係にあるのかを調べる手法として、主成分分析があり、それについては Chapter 12 で述べる。

参考文献

[1 ]. 日本統計学会,“統計学基礎 : 日本統計学会公式認定統計検定2級対応”, “東京図書”,2021

[2]. 中谷, 秀洋,“わけがわかる機械学習 : 現実の問題を解くために、しくみを理解する”, 技術評論社,2019

[3]. C. M. Bishop, 元田浩, 栗田多喜夫,樋口知之,松本裕治,村田昇, “パターン認識と機械学習 : ベイズ理論による統計的予測（上下）”,丸善出版,2012

演習

. 多項式近似を行うプログラムにおいて、以下のようにすると sin関数で近似を行うことができる。ここを様々な関数に変えて行ってみよ。

> func_sin <- function(a,x) sin(a*x)
> func_phi_sin <- function(a,x_n){
+   phi <- vector("list",length=a)
+   phi <- map(1:a,func_sin,x=x_n)
+   phi <- matrix(unlist(phi),ncol=a)
+   colnames(phi) <- str_c("x",1:a)
+   phi <- as_tibble(phi)
+ }