11 ニューラルネットワーク
人は学習することで、最初はできないこと機能を後から獲得することができる。 学習をモデル化し、データをもとに機械がその関係を学ぶ機械学習について、ニューラルネットワークを例に述べる。データからルールを学び予測する方法について説明する。
キーワード
機械学習、最急降下法、汎化、過学習
11.1 神経細胞の振る舞いとニューロンのモデル
脳は神経細胞、またはニューロン(neuron)が互いにつながり、 大規模なネットワークを形成している。このネットワークを神経回路網または、ニューラルネットワーク (neural network)という。 ニューロンは、一定以上の刺激を受けると「活動電位」と呼ばれる電気パルスを発生する。 発生した電気パルスは軸索(axon)と呼ばれる電気ケーブル上を伝播する。発生した電気パルスはこの伝播の過程において整形され、ほぼ一定の大きさになる。 ニューロンから伸びた軸索は途中枝分かれしながら、その終末では、シナプス(synapse)と呼ばれる結合点で 他のニューロンの細胞体や樹状突起につながっている。この結合をシナプス結合という。 一般的なシナプスでは化学伝達物質を介して、他のニューロンへ情報を伝える(Figure 11.1)。

神経細胞の振る舞いをまとめると次のようになる。
神経細胞は複数のパルスを受け取り複数のパルスを発生させる。 そのパルスの個数の変化のさせ方が神経細胞の特徴である。
神経細胞にはしきい値があり、神経細胞の振る舞いを特徴付ける変数の一つである。
到着したパルスが神経細胞にどう影響を与えるかを決めるのがシナプスであり、 この伝達効率が変わることで人は学習していると考えられている。
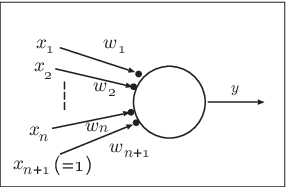
これをモデル化することを考える。パルス1つではなく、 ある時間幅の中にどれだけの電気パルスが来たのかという発火の割合を考えてみよう。 神経細胞には \(n\)個の入力があると考える。入力ごとに重みづけをして 合計し、その値によって出力の割合が変化すると考える。こうするとニューロンの振る舞いは
\[\begin{eqnarray} u&=&\sum_{i=1}^{n}w_ix_i -\theta \\ \nonumber y&=&f(u) \end{eqnarray}\]と書くことができる。ここで、\(\theta\) はしきい値を表すパラメータであると する。この\(f\) としては 代表的なものとしてはシグモイド関数や ReLU関数 (Rectified Line Unit) が用いられる。
\[\begin{eqnarray} {\rm sigmoid} (u) &=& \frac{1}{1+\exp(-au) } \\ {\rm relu}(u) &=& \left\{ \begin{array}{ccc} u &\;\;\;& u \geq 0 \\ 0 &\;\;\;& u < 0 \end{array} \right. \end{eqnarray}\]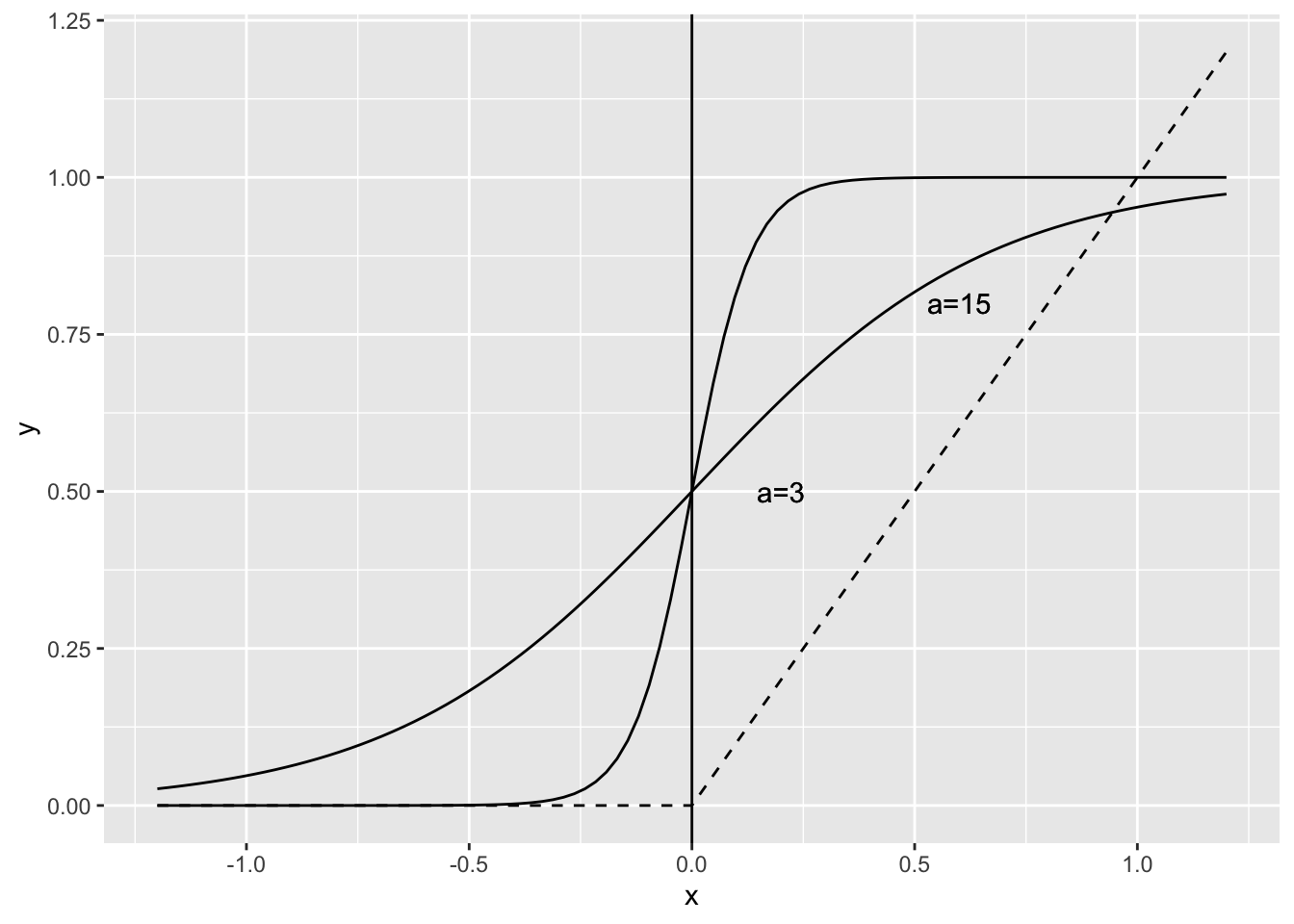
シグモイド関数は図1.4に示すようなS字型の関数である。 \(a\)の値が大きくなると、\(u\geq 0\)であれば出力が、ほぼ\(1\)、 \(u<0\)であれば出力としてはほぼ\(0\)というように 2値のニューロンのモデルと似た振る舞いを示すこともできる。
シグモイド関数は微分すると、 \[ f^{\prime} (u) = a f(u)(1-f(u)) \] となる。 このように、シグモイド関数は\(a\)の値によって、階段関数や直線に近い関数へと変えることができ、 また階段関数とは違って微分できるという特徴がある。
11.2 バックプロパゲーション
ここでは1987年にラメルハート(D.Rumelhart)によって提案されたバックプロパゲーションというモデルについて説明する。 この学習則を用いると出力層だけでなく、入力層から中間層へとつながる結合についても学習することが できるが、後に行うシミュレーションにおいては3層のネットワークを扱うの で、図(#fig-nnet-bp)に示すような ニューラルネットワークをもとに説明する。 今、入力の個数が \(n\)個(しきい値を含めて\(n+1\)個)、出力が\(m\)個であるとする。さらに例題の数が\(N\)個あるとしよう。 p番目 の入力 \(x\)\(^{(p)}\) tに対して、ニューラルネットワークの 出力を\(y\)\(^{(p)}\)、一方、本来出力してほしい値(これを教師信号という)を \(\hat{y}\)\(^{(p)}\)とする。 ここで、\(p\) は\(p\)番目の例題を意味することとする。
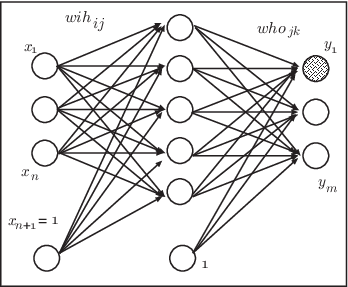
つまり、 \[ {\mathbf x}^{(p)}= \left( \begin{array}{c} x_1^{(p)}\\ x_2^{(p)}\\ \vdots\\ x_n^{(p)}\\ x_{n+1}^{(p)}(=1) \end{array} \right) , {\mathbf y}^{(p)}= \left( \begin{array}{c} y_1^{(p)}\\ y_2^{(p)}\\ \vdots\\ y_m^{(p)} \end{array} \right) , \hat{\mathbf y}^{(p)}= \left( \begin{array}{c} \hat{y_1}^{(p)}\\ \hat{y_2}^{(p)}\\ \vdots\\ \hat{y_m}^{(p)} \end{array} \right)\] である。 この時、バックプロパゲーション法では出力と教師信号との誤差の2乗を最小にしようとして学習する。
\[E_p=\sum_{k=1}^{m}(y_k^{(p)}-\hat{y}_k^{(p)})^2 \] \[E = \sum_{p=1}^{N}E_p \]
この時、結合荷重 \(w_i\)(\(wih_{ij}\)や\(who_{jk}\)) の 修正量 \(\Delta w_i\) は誤差 \(E\) を偏微分した値を用いて
\[\Delta w_i =-\epsilon \frac{\partial E}{\partial w_i} \]
のように修正する。 ここで \(\epsilon\) は用いた修正する大きさを決める変数である。 偏微分とは他の変数は無視して、その変数を変化させたときの関数の変化の量を表しているので、この値が正ということは、結合荷重を少し増やすと誤差が増えるということを意味している。 逆にその値が負であれば、結合荷重を増やすと 誤差が減るということである。 どちらにしても、偏微分した値の逆の方向に 結合荷重を変化させるということは、 必ず誤差を減らす (偏微分の値が \(0\) になって変化しない場合を含めて正確に言うと増やさない)方向に変化させることを意味している。 これは誤差の曲面に対して最も急な傾斜の方向へと修正を行うことから、 最急降下法 (gradient descent method)という。 そこで、結合荷重に対する2乗誤差が (Figure 11.5) のように表せるとして、 この学習のメカニズムについて考えてみよう。 先ほど計算した偏微分はその点における接線の方向に変化する。例えば 点Aから出発すると必ず誤差を増やさない方向に変化するので 徐々に \(w\) を増加させていく。\(\epsilon\) が十分小さい値であれば、 L1の地点では偏微分の値が \(0\) になるので、変化しなくなる。 同様に点CからスタートしたときにはL2の地点で学習が終わる。このように、最急降下法では必ずしも誤差が全体の最小値ではなく、局所的な最小値(極小値)で学習が終了するという欠点がある。
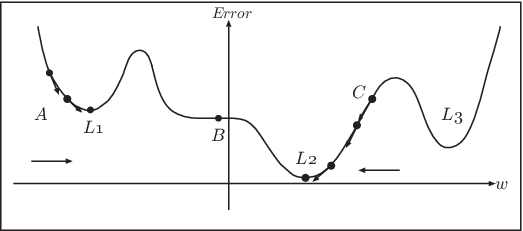
また、点Bは極小値ではないが、その場において偏微分の値が0になるところである。このような平坦な場でも学習が進まなくなるということが起こる。 このような平坦な場をプラトー(plateau)という。 式([eqn:err2] は出力層の場合には単純に計算することができる。また、誤差\(E\)の中間層\(wih\)による 偏微分の値についても合成関数の偏微分(連鎖律)の知識をもとに計算することができる (その計算の詳細については省略する)。 中間層が複数ある場合であっても同様に計算することができる。 その際、偏微分の値は出力層に近い方から計算し、出力層に近い中間層から入力層へ向かって逆方向へ順番に計算していく。 このように、誤差の情報が逆方向に伝わっていくことから、この学習則をバックプロパゲーション (back propagation)(または誤差逆伝播法)という。
11.3 汎化能力と過学習
ニューラルネットワークを用いて学習することのメリットとは、例題を用いて学習し、学習の結果、例題以外の問題に対しても 望むような出力を出すことである。これを汎化(generalization)能力という。 汎化能力について、図をもとに考えてみよう。
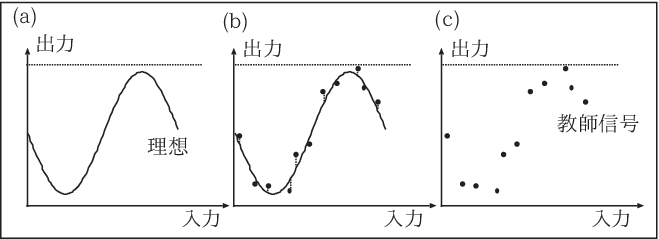
ニューラルネットワークは\(0\)から\(1\)の値を取る多入力多出力の関数であると考えることができる。 例として1入力1出力であるとし、横軸を入力、縦軸をネットワークの出 力であるとする。 図(#fig-nnetgeneral)(a) のような \(\sin\)曲線になるように関数にしたいとしても、実際には必ずしも多くのサンプルが得られるとは 限らない。また、その限られたサンプルも必ずしも正確な値とは限らず誤差を含むということもあるだろう( 図11-6(c))。
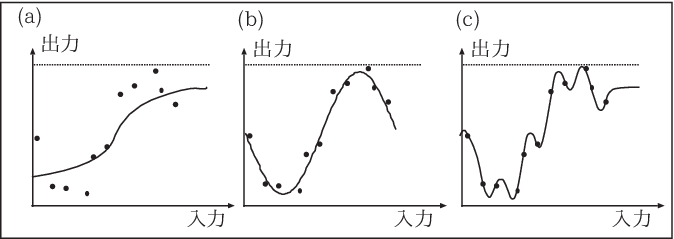
図11-7 (a)はそもそも学習ができていない場合である。極小値やプラトーなど、 途中で学習がストップしてしまった場合や そもそも中間層が少ない場合などに起こる。 一方、中間層の個数を増やしていくと、ネットワークとして表現できる能力があがっていき、 ノイズの部分まで正確に訓練してしまい、 図11-7(c)のように汎化能力が下がってしまう。 実際のデータにおいても、例題に対する学習は非常に小さいが、未学習の検証データに対する誤差が大きくなるということが起こる。 このように訓練データに過度に適合してしまう状態を過学習(overfitting)という。 実際にバックプロパゲーションを行う場合には、中間層が大きすぎると過学習が起こりうるので、 例題に対する訓練誤差が十分少なくなるネットワークのうち、 サイズの最も小さいネットワークが用いられる。 しかし、あらかじめ、中間層をどのぐらいの個数にするべきかがわかるということはあまりなく、ある程度試行錯誤が必要となる。 このようにニューラルネットワークは例題の中に隠れたルールを自動的に見つけ、 例題以外の入力に対しても 正解を導いてくれる可能性を有している。こうしたルールとは、 単に回帰分析で行ったような線形な関係だけでなく、非線形であってもよい。
11.4 Rによるシミュレーション
バックプロパゲーションのしくみやその特徴について述べた。そこで、次にRを用いて実際のデータに適用してみよう。 ここでは、nnetというパッケージを使う。library(nnet)でパッケージを読み出し、そのパッケージに 含まれるnnetという関数で学習をし、predictという関数を用いて、学習したネットワークが検証用の入力に 対してどのような出力をするのかをチェックする。具体的な手順は以下の通り。第9章で用いた \(\sin\)カーブを使うことにしよう。ただし、出力の範囲が \(0\) から \(1\) となるように 変更する。
> df_train <- df_train %>% mutate(y2 = (y+1)/2)- 学習を行う。
3層のニューラルネットワークのパッケージとして nnet があるという関数を使う。nnetは nnet(目的変数~説明変数、データ、中間層の数、最大学習回数) という形で引数を指定する。 sizeが中間層の個数、maxitが最大の学習回数となる。学習は誤差がある程度小さくなるか 最大学習回数に達するまで繰り返す。
> library(nnet)
> set.seed(10)
> sin1 <- nnet(y2~x1,data=df_train,size=5,maxit=1000)# weights: 16
initial value 2.543807
iter 10 value 0.372496
iter 20 value 0.329180
iter 30 value 0.260288
iter 40 value 0.203294
iter 50 value 0.067396
iter 60 value 0.054847
iter 70 value 0.049760
iter 80 value 0.046016
iter 90 value 0.039597
iter 100 value 0.035792
iter 110 value 0.028717
iter 120 value 0.028043
iter 130 value 0.024152
iter 140 value 0.019493
iter 150 value 0.019110
iter 160 value 0.018045
iter 170 value 0.017813
iter 180 value 0.017782
iter 190 value 0.017777
iter 200 value 0.017694
iter 210 value 0.017637
iter 220 value 0.017614
iter 230 value 0.017553
iter 240 value 0.017521
iter 250 value 0.017390
iter 260 value 0.017377
iter 270 value 0.017353
iter 280 value 0.017223
iter 290 value 0.017205
iter 300 value 0.016830
iter 310 value 0.016276
iter 320 value 0.016150
iter 330 value 0.015767
iter 340 value 0.014880
iter 350 value 0.014701
iter 360 value 0.014553
iter 370 value 0.013767
iter 380 value 0.013501
iter 390 value 0.013419
iter 400 value 0.013255
iter 410 value 0.012906
iter 420 value 0.012904
iter 430 value 0.012896
iter 440 value 0.012803
iter 450 value 0.012802
iter 460 value 0.012784
iter 470 value 0.012779
iter 480 value 0.012779
iter 490 value 0.012776
iter 500 value 0.012759
iter 510 value 0.012758
iter 520 value 0.012755
iter 530 value 0.012749
iter 540 value 0.012743
iter 550 value 0.012743
iter 560 value 0.012729
iter 570 value 0.012725
iter 580 value 0.012722
iter 590 value 0.012722
iter 600 value 0.012709
iter 610 value 0.012708
iter 620 value 0.012708
iter 630 value 0.012704
iter 640 value 0.012685
iter 650 value 0.012676
iter 660 value 0.012667
iter 670 value 0.012666
iter 680 value 0.012665
iter 690 value 0.012665
iter 700 value 0.012655
iter 710 value 0.012654
iter 720 value 0.012645
iter 730 value 0.012645
iter 740 value 0.012644
iter 750 value 0.012644
iter 760 value 0.012643
iter 770 value 0.012635
iter 780 value 0.012632
iter 790 value 0.012628
iter 800 value 0.012627
iter 810 value 0.012626
iter 820 value 0.012626
iter 830 value 0.012620
iter 840 value 0.012615
iter 850 value 0.012607
iter 860 value 0.012605
iter 870 value 0.012602
iter 880 value 0.012601
iter 890 value 0.012600
iter 900 value 0.012591
iter 910 value 0.012590
iter 920 value 0.012585
iter 930 value 0.012582
iter 940 value 0.012577
iter 950 value 0.012575
iter 960 value 0.012572
iter 970 value 0.012472
iter 980 value 0.012468
iter 990 value 0.012432
iter1000 value 0.012425
final value 0.012425
stopped after 1000 iterations- 予測を行う。 上記の作業によってできた
sin1には学習後の結合荷重の値が含まれている。 このネットワークを用いて検証用のデータで予測値を計算する。predict()を用いる。
> yosoku1 <-predict(sin1,newdata=df_test,type="raw")
> df_test <- df_test %>% mutate(nn_y=yosoku1[,1])ここで raw とは出力が実際の値である(クラス分けではない)ことを意味している。
これを図で確認しよう。次の例では func_sin2 として三角関数の曲線を定義して そこに訓練データと検証データを重ねて書いている。
> func_sin2 <- function(a,b,c,x) a*sin(b*x)+c
> ggplot() + xlim(0,1)+
+ geom_function(fun =func_sin2,
+ args=list(a=1/2,b=2*pi,c=0.5),col="gray60")+
+ geom_point(data=df_train,aes(x=x1, y=y2) ) +
+ geom_line(data=df_test,aes(x=x1, y=nn_y) ) 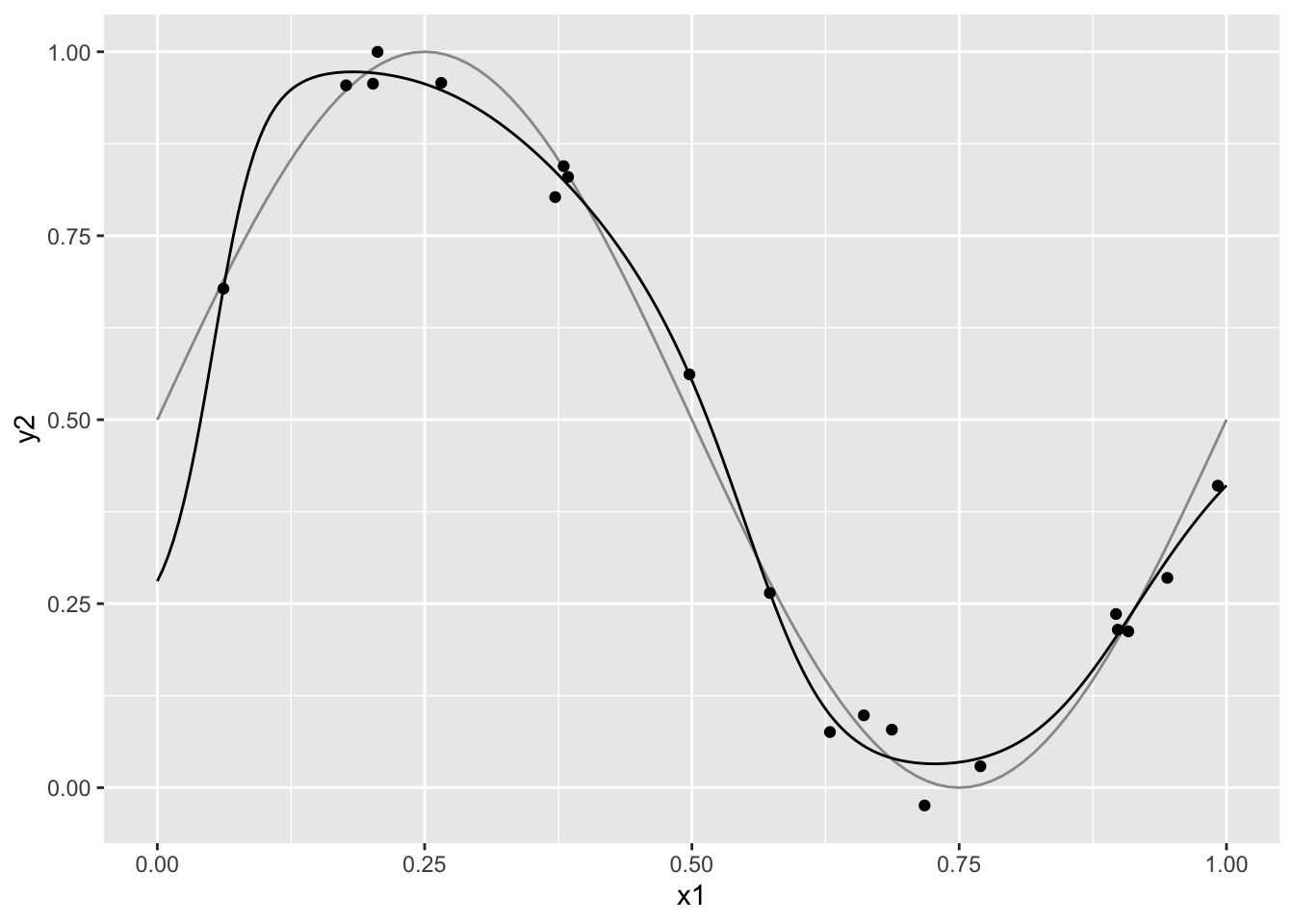
初期値がランダムに割り当てられるので、毎回必ずこのような結果になるわけではない。 サンプルデータや中間層の個数などを変えて試してみよう。
11.5 まとめ
ニューラルネットワークを用いた教師あり学習について述べた。ニューラルネットワークを用いることのメリットとは、
入力と正解のペアである例題をもとにして自動的に学習してくれること。
一つ一つの入出力を覚えるのではなく、適切な結合荷重の値を覚えることによって覚える容量を少なくすることができる。
例題以外の入力に関しても妥当な答を出す。
といったメリットがある。 しかし一方で、例題をもとにルールを再現してくれる入出力装置ではあるが、そのルールが具体的にどうであるかについてはブラックボックスのままである。そこで、でき上がった結合荷重などの値をもとにルールを推測することになる。 また, ここではパターンに対する2乗誤差を評価のための関数として、これを減らすように学習を行ったが、 こうした方法だけでなく、汎化能力を高めるための方法として、2乗誤差に、結合荷重の大きさなどのネットワークの複雑さを 制限するペナルティー項を付加して
\[(誤差評価関数)= (2乗誤差)+(ペナルティ項) \]
をもとに学習を行うことで枝刈りを行う方法も提案されている。
また、今回は主に予測の問題について扱ったが、バックプロパゲーションは予測以外にも判別の問題に応用することもできる。
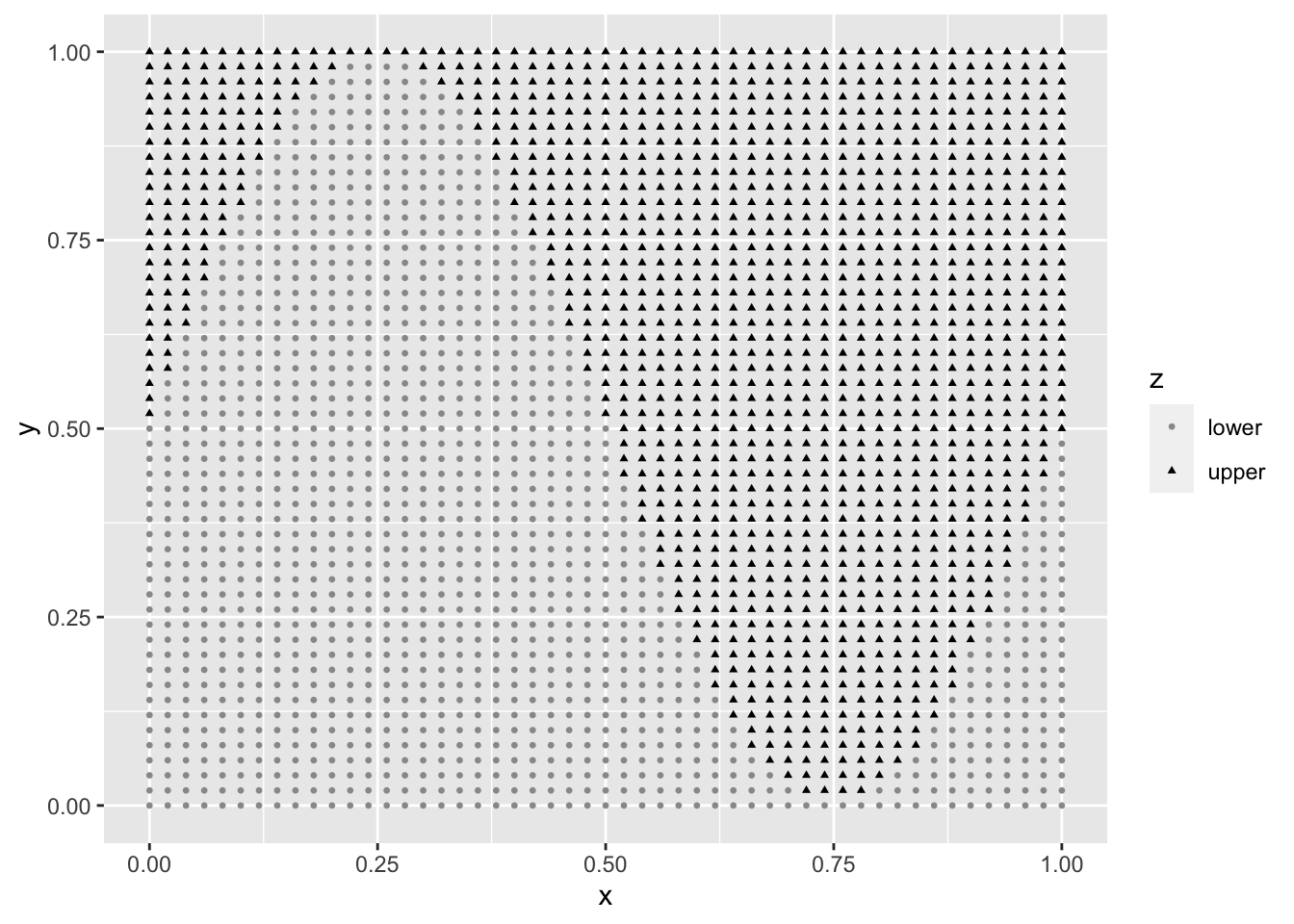
nnetというライブラリを用いる場合には、predict という関数で判別した値を出力する場合に、type="class" と指定することで判別の問題にも利用することができる。
参考文献
[1]. 金明哲,“Rによるデータサイエンス(第2版)”, 森北出版,2017
[2]. C. M. Bishop, 元田浩, 栗田多喜夫,樋口知之,松本裕治,村田昇, “パターン認識と機械学習 : ベイズ理論による統計的予測(上下)”, 丸善出版,2012
[3]. Chollet François,J. J. Allaire(著) 長尾高弘,瀬戸山雅人(訳), “RとKerasによるディープラーニング”,オライリー・ジャパン,2018
演習問題
- データで例題をもとに学習しても意味のないと思われる事例はないか考えてみよう。
(例) 電話帳のデータからいくつかのサンプルを取り出し学習させて、別の人の 電話番号を予測する
補足
今回は3層のニューラルネットワークについて説明した。シグモイド関数を用いた学習は層が増えると収束に時間がかかったり動作が上手くいかないことが知られている。構造を工夫することで その問題点を克服したのが 深層学習である。 深層学習を実装したものとして Python で書かれた Keras というライブラリーがある。 R でもrkeras というパッケージを用いて 深層学習を行うことができる([3])。
Google が提供している Colab https://colab.research.google.com/ は ブラウザ上で Python を動かすことができる環境である。 Google アカウントがあれば(放送大学の学生アカウントでも よい)無料で利用できる。 Colab は Jupytorノートブック と呼ばれるファイルに markdown と同じようにテキストとソースを書いて プログラムを実行する。
次のリンクをクリックするとプログラム言語を R と指定して 新しいノートブックを作成する。 https://colab.research.google.com/notebook#create=true&language=r または、まず、`ファイル`からノートブックをダウンロードする。
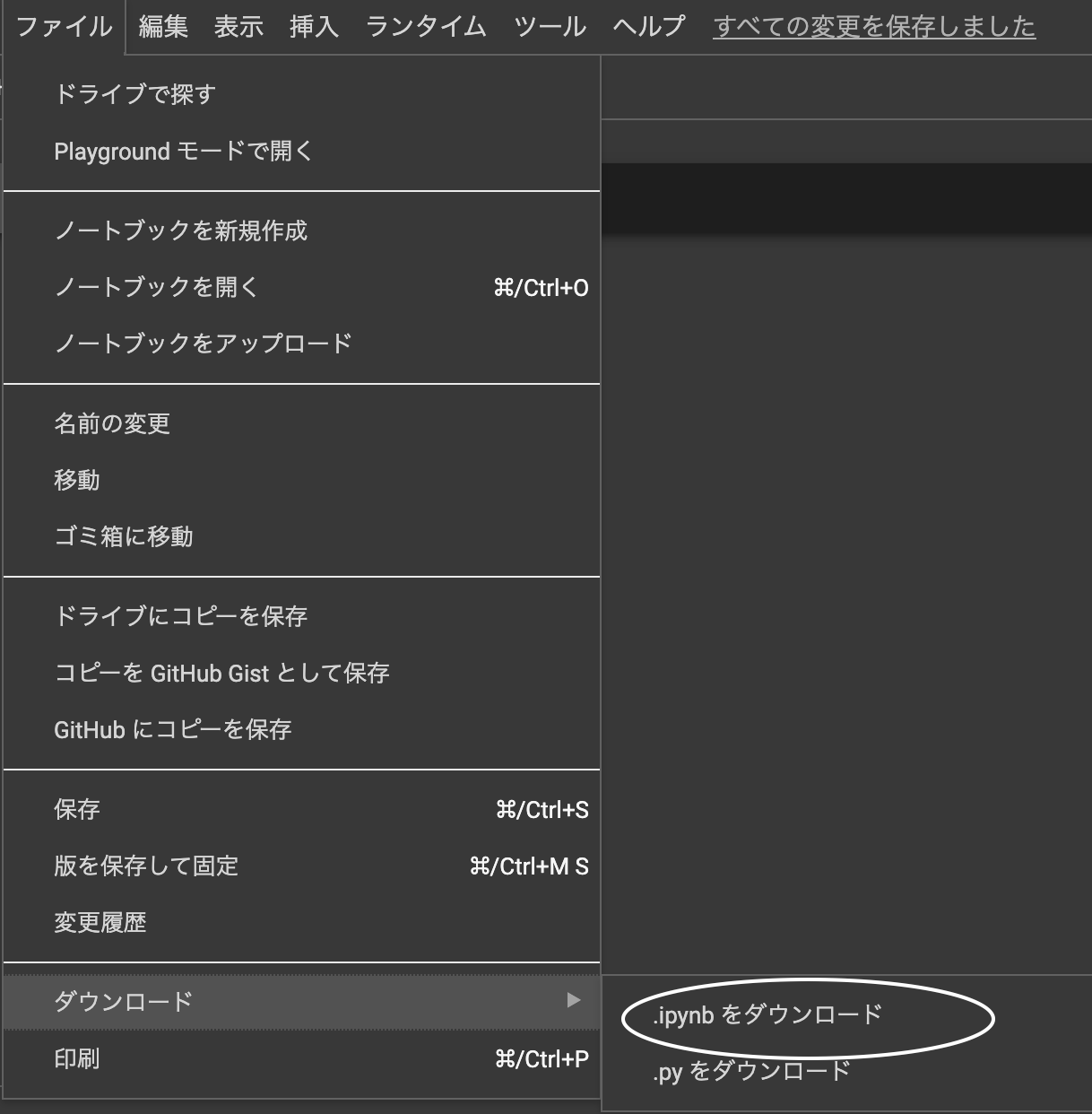
その後、RStudioのエディタで開き、
:ipynb の変更
"kernelspec": {
"name": "python3",
"display_name": "Python 3"
},
"language_info": {
"name": "python"
}
変更前
"kernelspec": {
"name": "ir",
"display_name": "R"
},
"language_info": {
"name": "R"
}
変更後
としてアップロードすると R言語を利用することができる。 そこでは rkeras などのパッケージがインストールされている。