14 距離データの可視化

要素間の距離が与えられたデータをグラフ化する方法について述べる。距離から座標を求める方法として多次元尺度法について述べる。また、後半では座標ではなく、樹形図として表す 階層的クラスター分析について述べる。

キーワード

距離の公理、樹形図、ヤングハウスホルダー変換、 ウォード法

14.1 距離の公理

アンケートをもとにして、人によって好みがどう違うかを分類するといったことを考えてみよう。そのためには、何らかの形で相手と似ているとか、離れているといったことが議論になる。そのためには、それぞれに対して違いに対応する「距離」が定義されていなければならない。では、距離とはどういうことなのだろうか。そこで、自宅から最寄りの学習センターまでどれだけ離れているのかを考えてみよう。通常、距離としてイメージされるものはユークリッド距離である。これは２点間を直線で結び、その長さを測ったものである。しかし、その他にも、例えば駅から徒歩何分であるという場合もあるだろう。この所要時間は距離といえるのであろうか。距離とは２点 $p$、$q$の間の関数を $d(p,q)$とする。このとき、以下の４つの性質を満たすとき、 $d(p,q)$ を距離という。

非負性:　$d(p,q)\geq 0$
対称性:　$d(p,q) = d(q,p)$
三角不等式:　3点$p$、$q$、$r$に対して $d(p,q)\leq d(p,r)+d(r,q)$
非退化性:　$p=q \Leftrightarrow d(p,q)=0$

この４つの性質のことを距離の公理という。

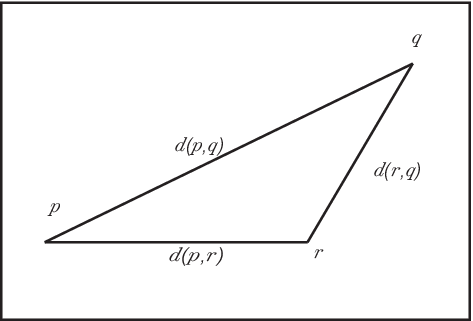
非負性とは、２点間の距離は負にはならないことである。非退化性とあわせて考えると、距離が0になるというのは出発点と到着点が同じであるときだけであり、それ以外の場合は距離が正となる¹。対称性について、例えば移動にかかる時間によって、距離を定義したいという場合、飛行機での移動時間では通常対称性が成り立たない (東京から北海道に行く時間と、北海道から東京へ行く時間は通常等しくない)。また、三角不等式の意味は、点$p$ から点 $q$ への距離とはその最短距離のことであり、途中の点 $r$を通った場合には、通り道にある場合を除いて遠回りになるということを意味している。
今後は原則としては距離の公理を満たすものとして話を進めるが、自分で距離を定義した場合には先ほど述べた公理を満たしているかどうかを検討する必要がある。

14.2 多次元尺度法の概略

数量化されたデータに対して、距離が定義されているものとしよう。このようにして距離だけが定義されているだけで、実際の座標が与えられていない、もしくは主成分分析で行ったように、座標が多次元で直接グラフにすることができない、という状況を考えてみよう。多次元尺度法とは、各対象同士の距離の情報を用いて、各点を空間内の点として表し、そのデータの構造を可視化するための方法である。実際にはデータ自体は多次元空間内で表されることが多いが、可視化するためには、２次元や３次元といった低次元の座標で表現する。ここでは古典的多次元尺度法(classical multidimensional scaling)について説明する。この後の計算では、主成分分析と同様に固有値や固有ベクトルを求めることになる。まず問題を定式化しよう。$r$ 次元の空間における $N$ 個の点に対し、2点間の距離が与えられているとしよう。その座標を表す行列$X$を

\[\begin{eqnarray} X &=& ({\mathbf x}_1,\cdots,{\mathbf x}_N)^T = \left( \begin{array}{ccc} x_{11}&\cdots&x_{1r} \\ \vdots&\ddots&\vdots \\ x_{N1}&\cdots&x_{Nr} \\ \end{array} \right ) \end{eqnarray}\]

とする。ここで、距離$d_{ij}$ としてユークリッド距離を考えよう。すると、各点の座標を表すベクトル ${\mathbf x}_i$、${\mathbf x}_j$ を用いて、

\[\begin{eqnarray} d_{ij}^2 = \sum_{k=1}^r (x_{ik}-x_{jk})^2 = {\mathbf x}_i\cdot{\mathbf x}_i + {\mathbf x}_j\cdot{\mathbf x}_j -2 {\mathbf x}_i\cdot{\mathbf x}_j \end{eqnarray}\]

と書くことができる。${\mathbf x}_i\cdot{\mathbf x}_j$ は内積を表す。また、$d_{ij}$を成分とする行列を$D$とし、$d_{ij}^2$を成分とする次のような距離行列を$D^{(2)}$とする²。

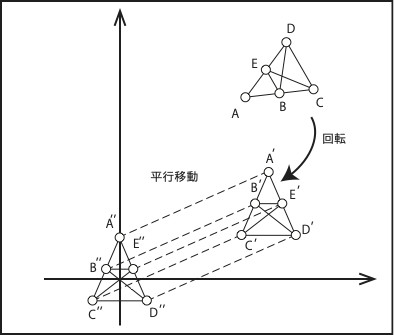
\[\begin{eqnarray} D^{(2)} &=& \left( \begin{array}{ccccc} 0 &d^{2}_{12} &d_{13}^2&\cdots& d_{1N}^{2}\\ d^{2}_{21} &0&d^{2}_{23}&\cdots& d_{2N}^{2}\\ d^{2}_{31} &d^{2}_{32} &0 &\cdots &d_{3N}^{2} \\ \vdots&\vdots&\vdots &\ddots&\vdots \\ d^{2}_{N1} &d^{2}_{N2} &d^{2}_{N3}&\cdots&0 \\ \end{array} \right ) \end{eqnarray}\]

多次元尺度法では、この$D^{(2)}$の値が得られているときから、$X$ を求めようとするものである。しかし、距離が与えられているからといって、座標が1つに求められるわけではない。 (Figure 14.2) を見ると、点を平行移動しても、回転しても、五角形ABCDEの２点間の各距離は変わらない。そこで、距離が$D^{(2)}$ が成り立つような $X$ の候補の1つを求めることを考える。

$D^{(2)}$は、 \[ D^{(2)} = {\mathbf {diag}}(X X^T)\cdot ({\bf 1}\cdot{\bf 1}^T) -2X X^T \\ \nonumber +({\bf 1}\cdot{\bf 1}^T)\cdot{\mathbf {diag}}(X X^T) \] と書くことができる。ここで、diag はその対角成分だけを取り出し、残りを $0$とすることを意味している。ここで、 \[{\mathbf 1} = \left( \begin{array}{c} 1\\ 1\\ \vdots \\ 1 \end{array} \right) \] であり、 \[ {\mathbf 1} \cdot {\mathbf 1}^T = \left( \begin{array}{ccc} 1&\cdots&1 \\ \vdots&\ddots&\vdots \\ 1&\cdots&1 \\ \end{array} \right ) \] である。そこで、この距離行列に対して、

\[\begin{eqnarray} Q = I- \frac{{\mathbf 1} \cdot {\mathbf 1}^T }{N} \end{eqnarray}\]

という行列 $Q$ を両側から掛ける。これを ヤング・ハウスホルダー(Young-HouseHolder)変換という。この操作を施すと、 \[ -\frac{1}{2} (Q D^{(2)} Q) =QXX^TQ \]

が成り立つ。ここで、$Q$ も$D^{(2)}$も対称行列であるので、この両辺も対称行列である。この変換は次のように解釈することができる。

\[\begin{eqnarray} M =\frac{{\mathbf 1} \cdot {\mathbf 1}^T }{N} &,& Y= ( {\mathbf y}_1 ,\cdots, {\mathbf y}_N )^T \end{eqnarray}\]

とする、$MY$ はそれぞれのベクトルに対して重心となるベクトルを求めている。したがって、$Q$ は $N$ 個の全ての点を重心が原点にくるように移動させる演算である。さて、今、$D^{(2)}$はわかっているので、$QD^{(2)}Q$を計算することができる。ここで対称行列の固有値は全て実数で、固有ベクトルは互いに直交するので、ここでこの対角行列を逆行列とするような固有ベクトルを選ぶことができる。ただし、距離のみが分かっている場合にＮ個の点のうち、独立なものは $N-1$個しかなく、固有値の 1つは$0$になる。

\[\begin{eqnarray} -\frac{1}{2}(QD^{(2)}Q)&=& P \left( \begin{array}{cccc} \lambda_1 &\cdots&\cdots& 0\\ \vdots &\ddots&\vdots &\vdots\\ 0&\cdots&\lambda_{N-1}&0 \\ 0&\cdots&0 & 0 \end{array} \right ) P^T \end{eqnarray}\]

と変形することができる。ここで、この固有値がすべて0以上であれば、 \[ Z= P \left( \begin{array}{cccc} \sqrt{\lambda_1} &\cdots& 0 & 0\\ \vdots &\ddots&\vdots &\vdots \\ 0&\cdots&\sqrt{\lambda_{N-1}} &0 \\ 0&\cdots&0 &0 \end{array} \right ) \] すると、$QX(QX)^{T}=ZZ^{T}$であり、 $Z$ を解の1つとして選ぶことができる。

14.3 Rによる多次元尺度法

R では距離形式のデータとして　UScitiesDがある。これはアメリカの都市間の距離のデータである。 dist 形式は対角成分が 0 の対称行列をしている。距離形式のデータを表示するには UScitiesD と変数名を打てば中身を表示できる。以下の例では行列形式にして先頭の6行だけを表示している。

> UScitiesD %>% as.matrix %>% head()

           Atlanta Chicago Denver Houston LosAngeles Miami NewYork SanFrancisco
Atlanta          0     587   1212     701       1936   604     748         2139
Chicago        587       0    920     940       1745  1188     713         1858
Denver        1212     920      0     879        831  1726    1631          949
Houston        701     940    879       0       1374   968    1420         1645
LosAngeles    1936    1745    831    1374          0  2339    2451          347
Miami          604    1188   1726     968       2339     0    1092         2594
           Seattle Washington.DC
Atlanta       2182           543
Chicago       1737           597
Denver        1021          1494
Houston       1891          1220
LosAngeles     959          2300
Miami         2734           923

> us1 <- cmdscale(UScitiesD,eig=T)
> us1

$points
                    [,1]       [,2]
Atlanta        -718.7594  142.99427
Chicago        -382.0558 -340.83962
Denver          481.6023  -25.28504
Houston        -161.4663  572.76991
LosAngeles     1203.7380  390.10029
Miami         -1133.5271  581.90731
NewYork       -1072.2357 -519.02423
SanFrancisco   1420.6033  112.58920
Seattle        1341.7225 -579.73928
Washington.DC  -979.6220 -335.47281

$eig
 [1]  9.582144e+06  1.686820e+06  8.157298e+03  1.432870e+03  5.086687e+02
 [6]  2.514349e+01 -8.116566e-10 -8.977013e+02 -5.467577e+03 -3.547889e+04

$x
NULL

$ac
[1] 0

$GOF
[1] 0.9954096 0.9991024

k=2 で座標の次元を指定する。また、eig=T とすると固有値を出力する。座標は us1$points に出力される。 GOFとは当てはまりの良さを表す指標である。 kで指定した個数の固有値まで累積和がすべての固有値の絶対値の和の中に占める割合を意味している。距離の公理を満たしていないデータなどの場合には負の固有値が出てくることもある。 GOF の2つの値は負の固有値を正とした場合と負の固有値を 0 とみなした場合の２種類で計算している。省略された場合には k=2,e=Fと判断し各点の2次元の座標だけが出力される。あとはこれをグラフにすればよい。nudgeは

> us2 <- tibble(name=rownames(us1$points),
+    x=us1$points[,1], y=us1$points[,2])
> ggplot(us2,aes(x=x,y=y)) + geom_point() +
+   geom_text(aes(label=name),vjust=1)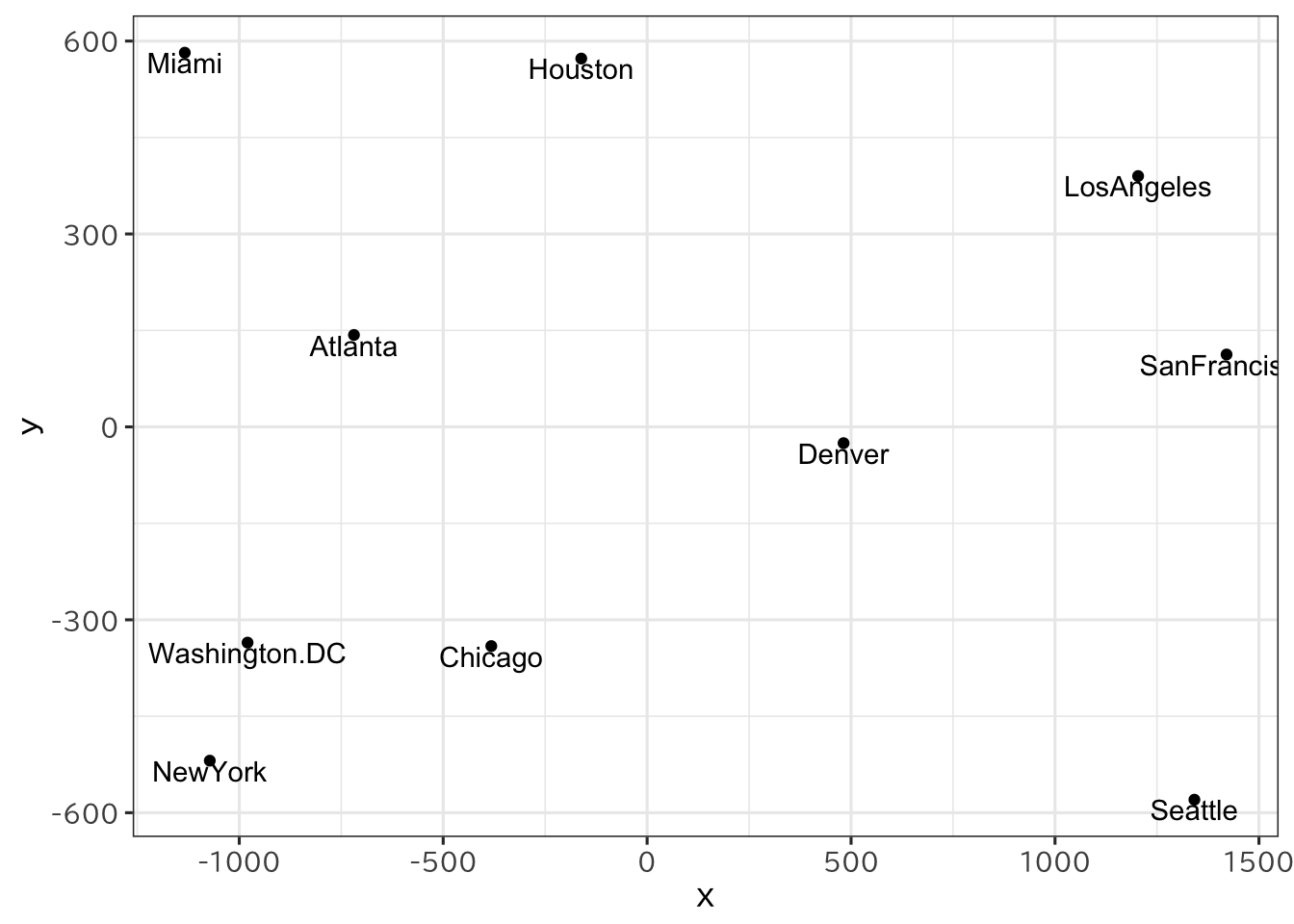

2点間の距離という情報をもとに点の座標を求め、 2次元などのグラフで表現するための手法について述べた。可視化すれば、どういったものが近くにあるかどうかを目で見ることができる。しかし、それでもグラフとして目で１度に見ることができるのは 3次元までである。データによっては必ずしも3次元以下で配置することができない場合もある。

14.4 階層的クラスター分析

実際にはこのような図ではなく、どれとどれが近いのかというグループだけがわかればよいこともある。このグループのように似た特徴を持つまとまりをクラスター(cluster)という。ここでは、こうしたクラスターに分割する方法について説明する。 階層的クラスター分析(Hierarchal Cluster Analysis) とは最も距離の近いものを 1つのクラスターとしてまとめ、順番にそのクラスターを結合していき、階層構造にまとめる手法のことである。この手順は (Figure 14.3) に示すことができる。

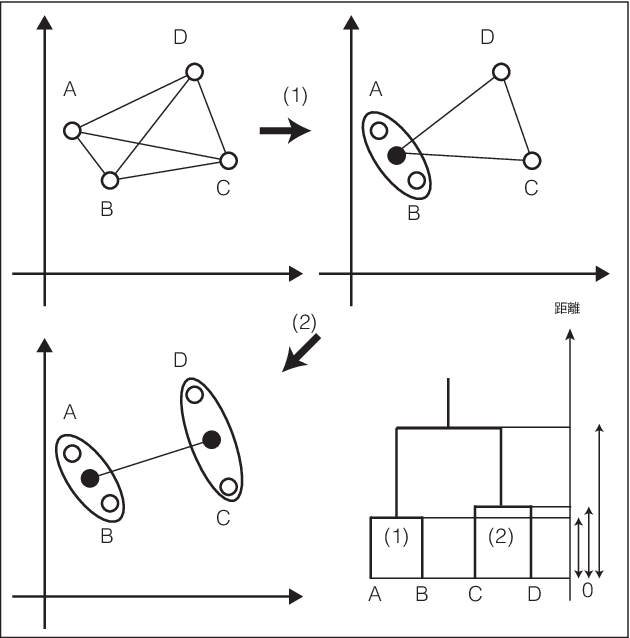
この手法では、

まず、 2つずつ組み合わせごとの距離を計算する。
最も距離の近いものを1つのクラスターとする。これによって、$n$ 個の要素から成っていたとすると、$n-1$個の点へと変わる。
このようにして 1つ減った要素に対して、あらためてそれぞれの距離を計算する。

という作業を繰り返すことになる。これを図にしたものが図1.1である。 (Figure 14.3) の右下のように構造をまとめた図のことを 樹形図(dendrogram)という。樹形図の高さが点を結合した際の距離を表している。
ここでの計算のポイントは、図に示すように点を結合してできたクラスターと他の点との距離をどうするか、ということである。あらためて距離を定義し直すにしても、クラスターが似た特徴を持ったものの集まりとなるように点の距離を定め直さなければならない。こうした距離の定め方として以下の5つの方法がよく知られている。

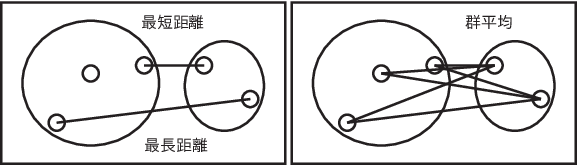
最長距離法 　 2つのクラスター間のすべての点同士の距離のうち、最も距離が長いものをクラスター間の距離とする方法。
最短距離法　 2つのクラスター間のすべての点同士の距離のうち、最も距離が小さいものをクラスター間の距離とする方法。
群平均法　 2つのクラスター間のすべての点同士の距離の平均を計算し、その距離の平均をクラスター間の距離とする方法。

重心法　図14-4 に示すように、それぞれのクラスターの重心の点を新たにそのクラスターの代表点として定め、それぞれの代表点同士の距離を求める方法。
ウォード法　クラスターが大きくなりすぎないように、クラスター内の距離の平方和(距離の2乗の和)が最も増えないようなクラスターを作成する方法。最短距離法の場合、クラスターの内側に他のクラスターの点と近いものがあれば、それが最短距離として採用されクラスターを結合する。このようなことを繰り返していくと、クラスターが点を吸収してどんどんと大きくなる。すると鎖状の樹形図が作られやすいという傾向がある（(Figure 14.5) (a) 参照）。これを鎖状効果(chain effect) という。しかし、近いもの同士が形成している集団を見つけだしたいという場合もある。そこでウォード法は、クラスター内の距離の2乗の和を計算し、この値が最も増えないような点を追加する。そこで点を付け加えたらクラスター内の距離の和がどれだけ増えるかという値を計算し、これを距離の代わりにする。

以上、グループ間の距離の計算について説明した。このように、点を結合して1つのグループとするたびに距離を計算し直す。そのため、点を結合したことによって、クラスター間の距離が前よりも短くなるということもある。樹形図においては、高さが点と点の距離を表す。この高さは、最初の点と点との距離ではなく、最終的に結合をするときの距離を利用している。したがって、樹形図で上下が逆になるということも起こる。これを距離の逆転という((Figure 14.5) (c) 参照)。

14.5 Rによるシミュレーション

Rには距離データとして、ヨーロッパの都市の道路距離のデータとしてeurodist がある。これを樹形図で表してみよう。

> eurodist %>% as.matrix %>% head()

          Athens Barcelona Brussels Calais Cherbourg Cologne Copenhagen Geneva
Athens         0      3313     2963   3175      3339    2762       3276   2610
Barcelona   3313         0     1318   1326      1294    1498       2218    803
Brussels    2963      1318        0    204       583     206        966    677
Calais      3175      1326      204      0       460     409       1136    747
Cherbourg   3339      1294      583    460         0     785       1545    853
Cologne     2762      1498      206    409       785       0        760   1662
          Gibraltar Hamburg Hook of Holland Lisbon Lyons Madrid Marseilles
Athens         4485    2977            3030   4532  2753   3949       2865
Barcelona      1172    2018            1490   1305   645    636        521
Brussels       2256     597             172   2084   690   1558       1011
Calais         2224     714             330   2052   739   1550       1059
Cherbourg      2047    1115             731   1827   789   1347       1101
Cologne        2436     460             269   2290   714   1764       1035
          Milan Munich Paris Rome Stockholm Vienna
Athens     2282   2179  3000  817      3927   1991
Barcelona  1014   1365  1033 1460      2868   1802
Brussels    925    747   285 1511      1616   1175
Calais     1077    977   280 1662      1786   1381
Cherbourg  1209   1160   340 1794      2196   1588
Cologne     911    583   465 1497      1403    937

Rには、階層的クラスターを行う関数にhclustがある。 hclust()はこの距離形式のデータを入力として用いる。plot() とすると、データから樹形図を書いてくれる。

> ed_co <- hclust(eurodist)
> plot(ed_co)

ggplot2 のスタイルで樹形図を書くには ggdendroというパッケージを使う。dendro_data()という関数を使うと、必要な情報をリストとして出力してくれる。

> library(ggdendro)
> den_ed_co <- dendro_data(ed_co)
> head(den_ed_co$segments,n=5L)

     x    y xend yend
1 4.25 4532  1.5 4532
2 1.50 4532  1.5  817
3 1.50  817  1.0  817
4 1.00  817  1.0    0
5 1.50  817  2.0  817

> head(den_ed_co$labels,n=5L)

  x y     label
1 1 0    Athens
2 2 0      Rome
3 3 0 Gibraltar
4 4 0    Lisbon
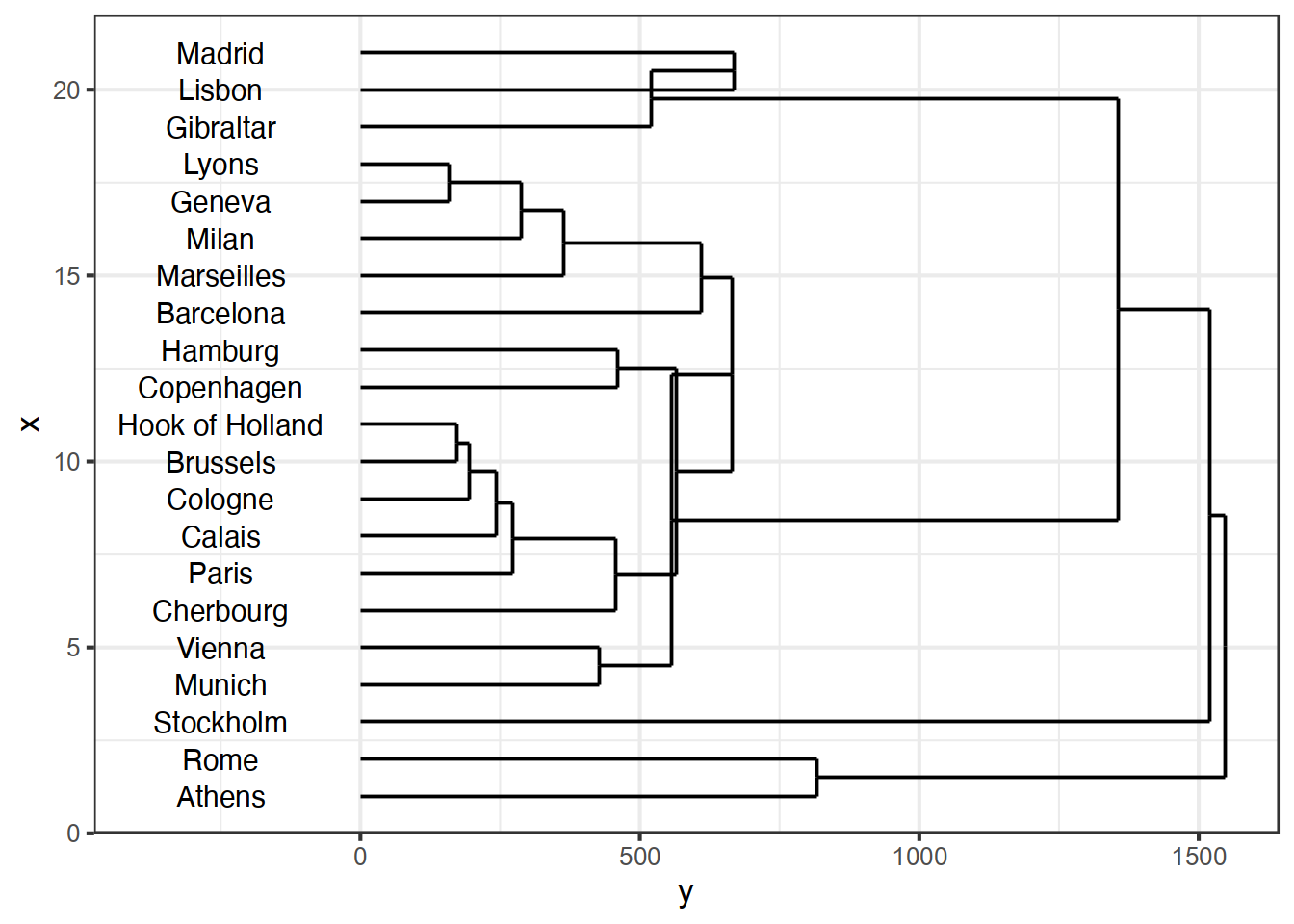
5 5 0    Madrid

den_ed_co には座標と名前がある。それをもとに　geom_segmentでは両端の座標を指定して線分を書き、geom_text で座標を指定して文字を書く。さらに文字を書く$y$ 座標を少ししたにずらした後に文字が潰れないように、coord_flip()で回転させて表示している。

> ggplot(data=segment(den_ed_co))+
+   geom_segment(aes(x = x, y = y, xend = xend, yend = yend) )+
+   geom_text(data = label(den_ed_co), 
+             aes(x = x, y = y-500, label = label),size=4) +
+   coord_flip()+
+   ylim(-600, max(den_ed_co$segments$yend) )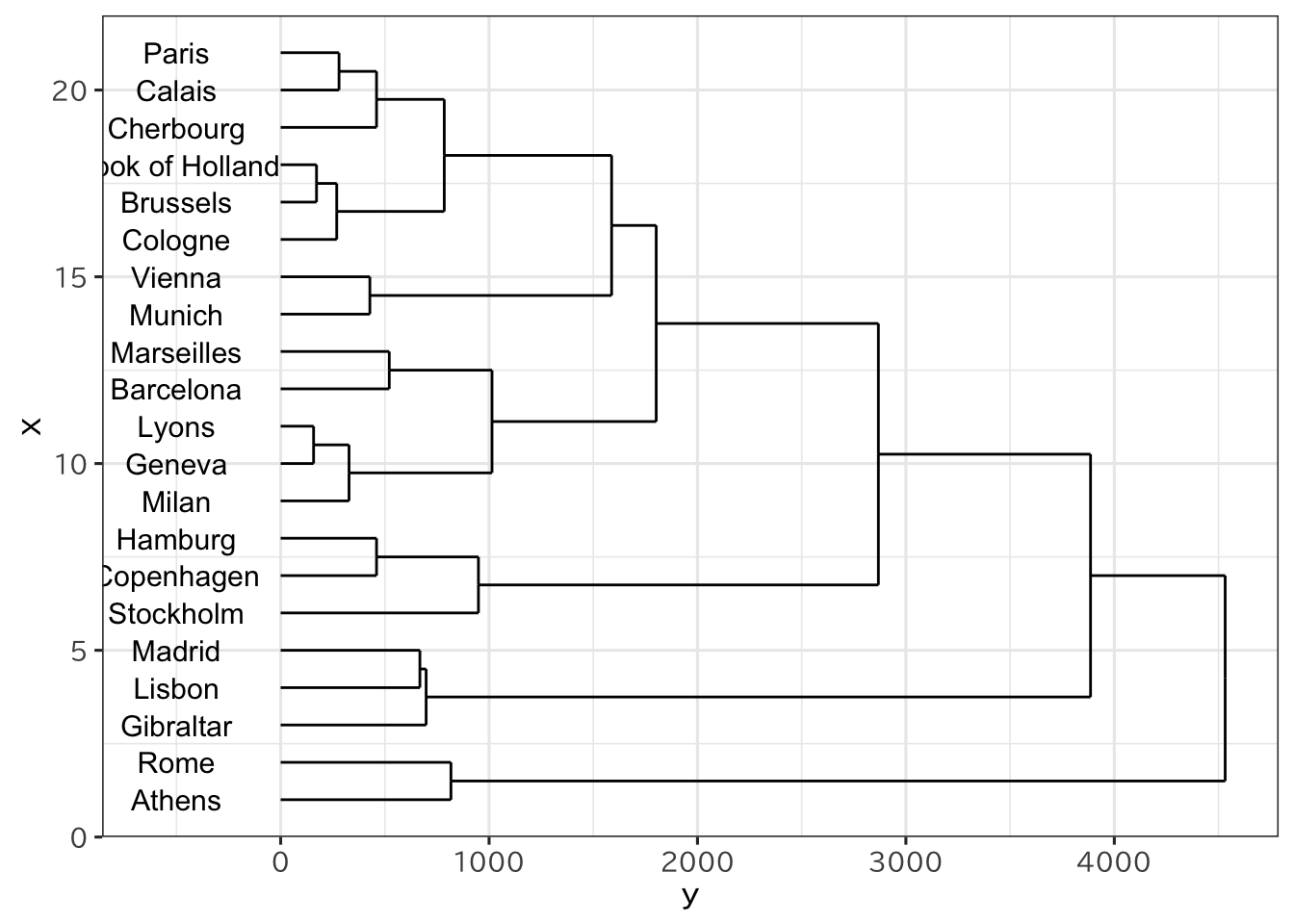

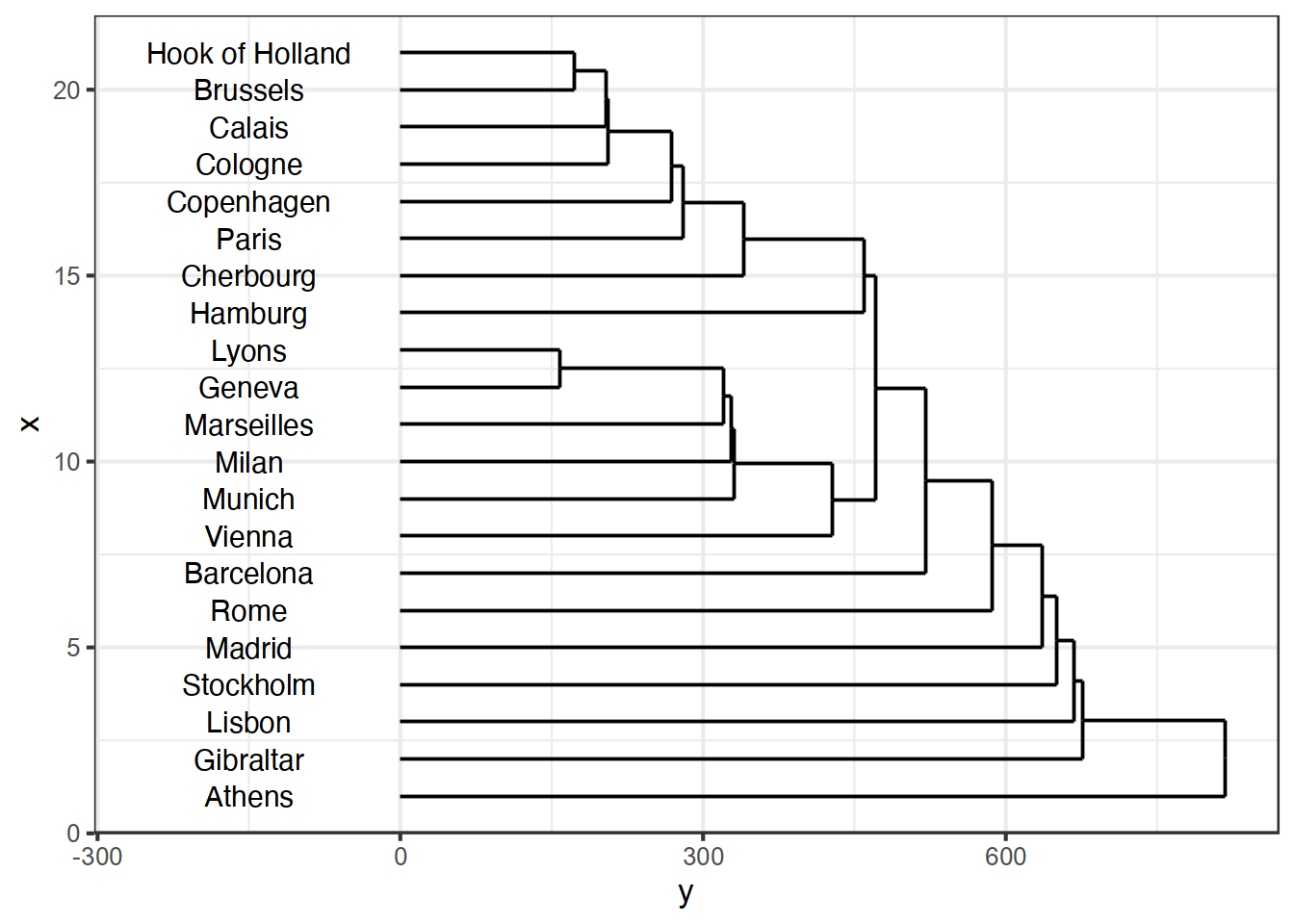
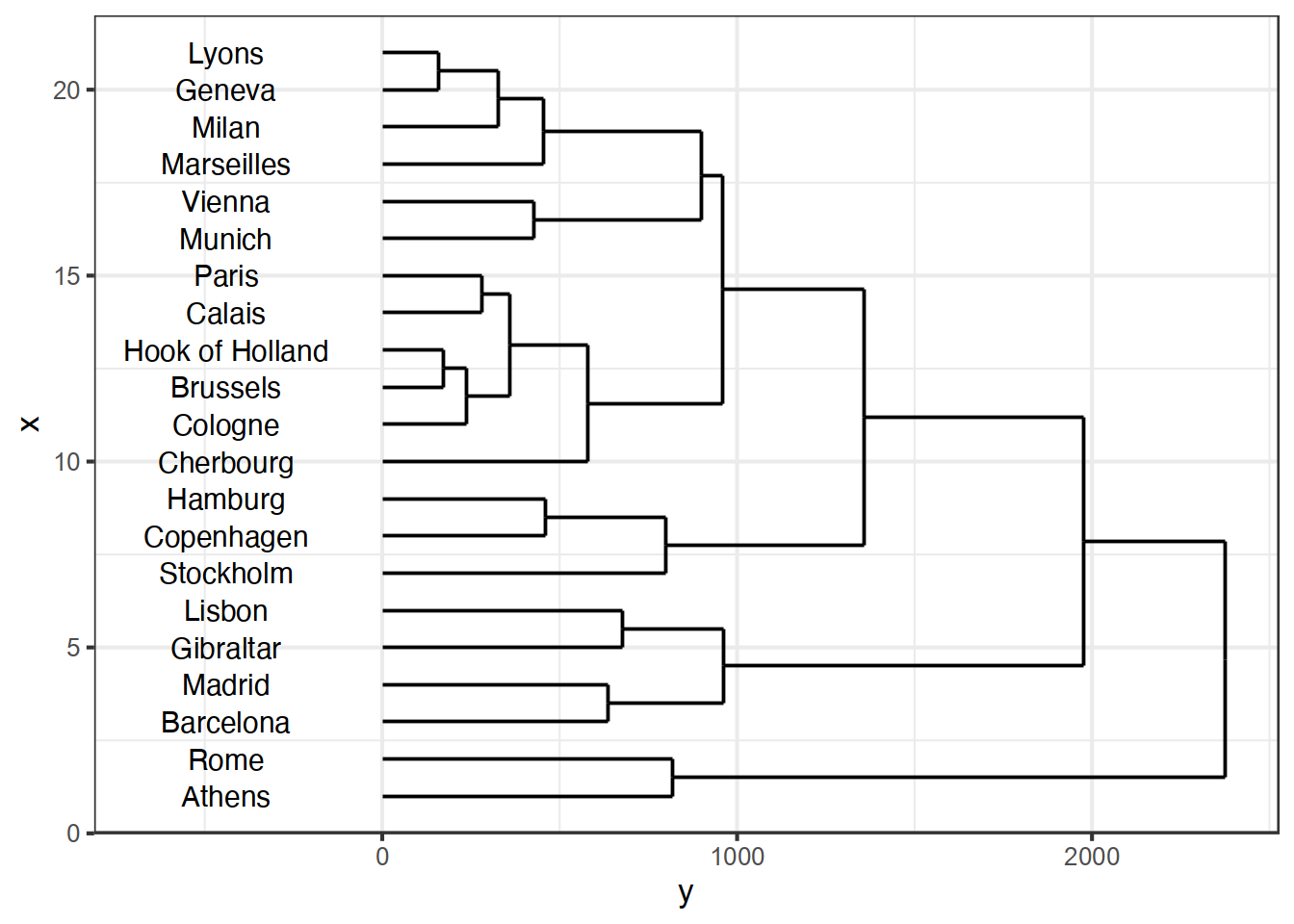
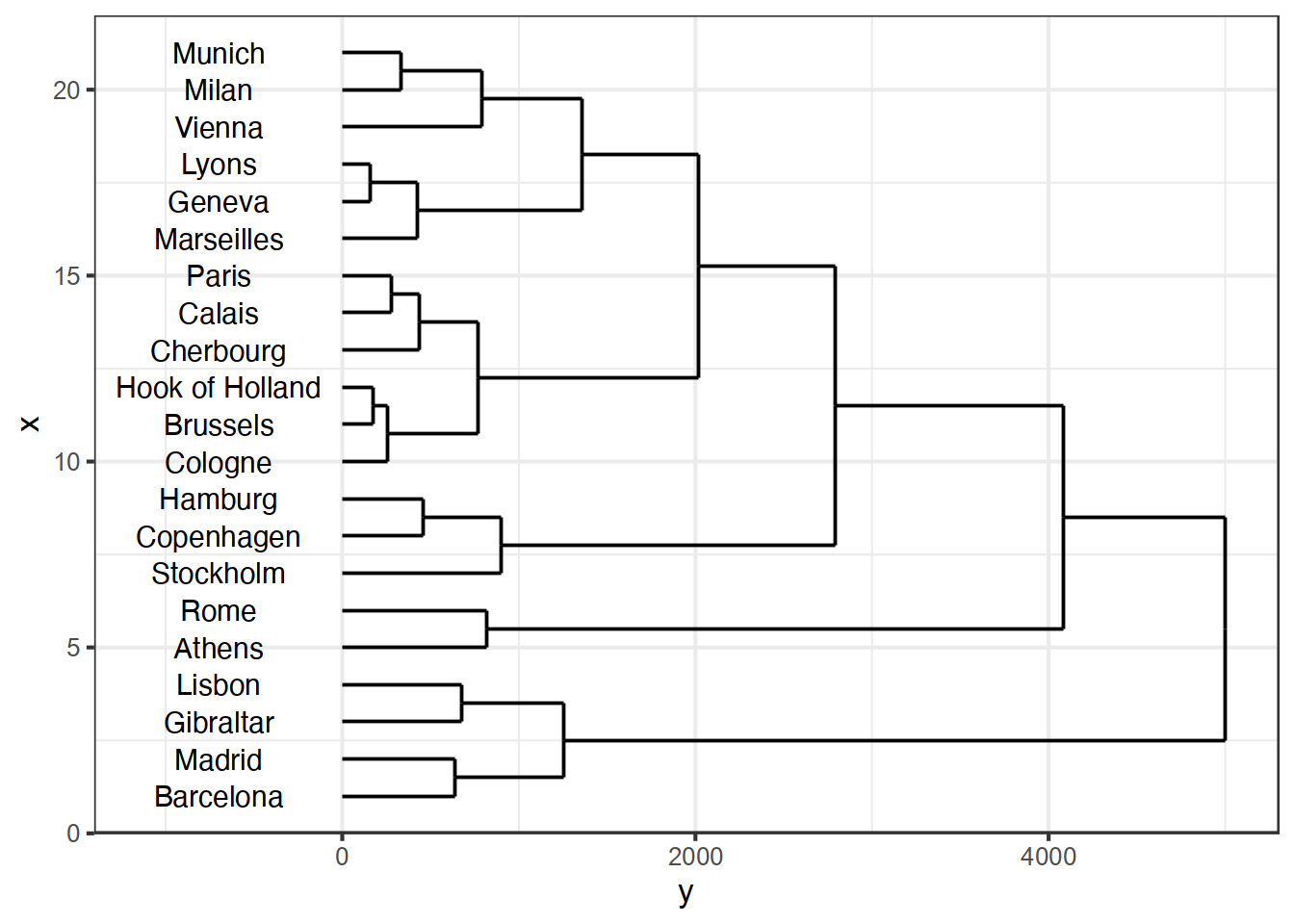
hclustで、距離を計算する方法を指定する場合には、method=で指定する。何も指定しないと最長距離法になる。例えばウォード法であれば、

> ed_wa <- hclust(eurodist,method="ward.D2")

と指定する。他の場合であれば、表1.1のように指定する.

Table 14.1: `hclust`での方法の指定
方法	引数
最短距離法	`single`
最長距離法	`complete`
群平均法	`average`
重心法	`centroid`
ウォード法	`ward.D2`

14.6 まとめと展望

この章では距離データを可視化する２つの方法について説明した。固有値、固有ベクトルを求めることによって、回転と平行移動ということについての自由度はあるが、互いの距離をもとにデータの座標を求めることができるという手法であった。また、もう一つの方法として樹形図で表す方法を説明した。樹形図を書いてクラスターのまとまり具合を図でみたあとに Chapter 15 で説明するようにある個数のグループに分類するということもできる。

参考文献

[1] 中村,永友,Rによるデータサイエンス2『多次元データ解析法』, 共立出版,2009

[2]. 林賢一,下平英寿,Rで学ぶ統計的データ解析,講談社,2020

[3]. 金明哲,“R によるデータサイエンス(第2版)”,森北出版,2017

演習

座標のデータから距離を求める関数として dist 行列形式で与えられたデータから右三角のデータへと直すものとして as.distという関数がある。

> a <- data.frame(id=1:5,x=rnorm(5),y=rnorm(5),z=rnorm(5))
> dist(a[,-1])

         1        2        3        4
2 2.649170                           
3 3.087769 3.281198                  
4 2.957523 2.588952 2.624392         
5 2.008021 2.717346 1.474003 3.011096

転置行列と元の行列を足すと対称行列になるので、そこから対角成分を2倍して、仮に距離の行列とすると、どういう操作をしているのかを確認できる。

> b <- matrix(runif(25),ncol=5) 
> c <- b+t(b)-2*diag(b)*diag(5)
> c

          [,1]      [,2]      [,3]      [,4]      [,5]
[1,] 0.0000000 1.2721546 0.7726062 1.4206173 0.4648486
[2,] 1.2721546 0.0000000 1.0544960 1.8290896 0.8250049
[3,] 0.7726062 1.0544960 0.0000000 0.8610462 0.7160058
[4,] 1.4206173 1.8290896 0.8610462 0.0000000 1.4071828
[5,] 0.4648486 0.8250049 0.7160058 1.4071828 0.0000000

> as.dist(c)

          1         2         3         4
2 1.2721546                              
3 0.7726062 1.0544960                    
4 1.4206173 1.8290896 0.8610462          
5 0.4648486 0.8250049 0.7160058 1.4071828

２点が異なる点に対して距離が$0$になることがあるとき、つまり、 $p=q \Rightarrow d(p,q)=0$が成り立つ場合を、擬距離という。↩︎
今、距離の2乗を成分とすることから$(2)$と書いたが、$D$の2乗という意味ではない。$D^2$を計算しても、$D^{(2)}$とは一致しないので注意しよう。↩︎